Introduction à la continuité et à la courbure dans SOLIDWORKS (Partie 1)

À travers SOLIDWORKS, on voit souvent des options permettant de rendre les éléments « tangents » ou « à courbure continue » (ou d'autres options similaires). Ces options sont présentes dans l'esquisse et la création de fonctions solides/surfaciques, mais leur définition mathématique est moins évidente. Apprendre à gérer correctement la continuité et la courbure dans SOLIDWORK est essentiel pour créer des conceptions aux facteurs de forme de haute qualité. Dans cet article, nous allons approfondir la nature mathématique de la continuité et de la courbure, ainsi que leur utilisation dans l'environnement SOLIDWORKS.

Types de continuité

Les ordres de continuité présents dans SOLIDWORKS sont les suivants : continuité de contact (C-0), continuité de tangente (C-1) et continuité de courbure (C-2). Pour illustrer ces concepts, nous allons examiner leur application aux entités d'esquisse 2D, notamment entre un arc et une ligne.

Continuité des contacts (C-0)

Le terme « continu » est défini par Merriam-Webster comme « marqué par une extension ininterrompue dans l'espace, le temps ou une séquence ». Pour notre propos, nous considérerons la continuité comme le simple fait qu'une entité commence là où la précédente se termine. Dans les images ci-haut, la ligne et l'arc avec un espace entre les extrémités sont discontinus. Dans l'autre ensemble, l'arc commence exactement là où la ligne se termine. On parle alors de continuité de contact ou de continuité « C-0 ».

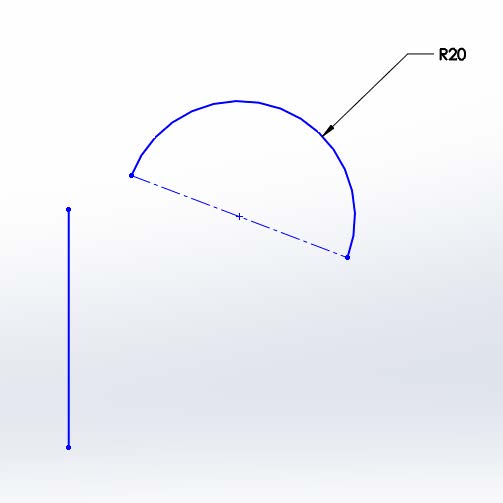
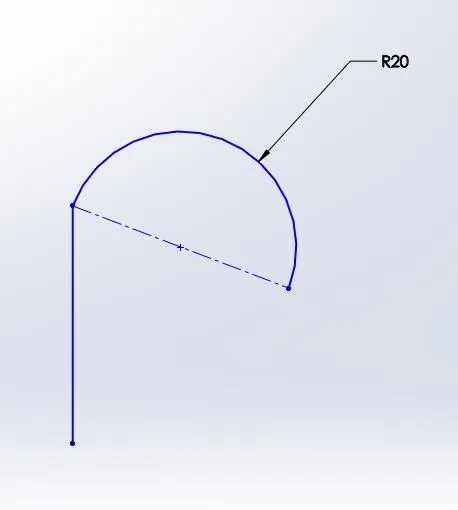
Discontinu  ...

Continuité tangente (C-1)

L'ordre de continuité suivant présente une continuité de contact (C-0), mais maintient également la continuité de trajectoire. Autrement dit, au sommet entre les deux entités, celles-ci sont instantanément parallèles. Ceci est généralement obtenu par une relation tangente lors du dessin.

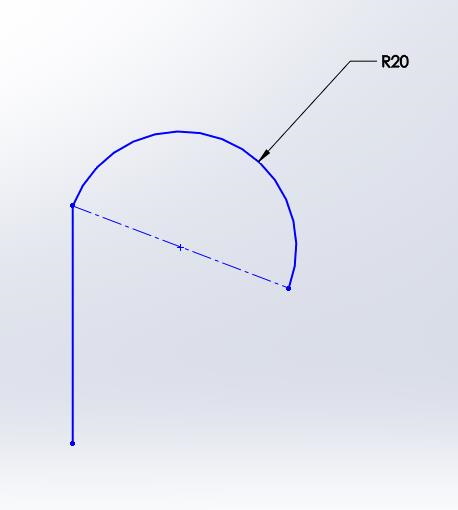
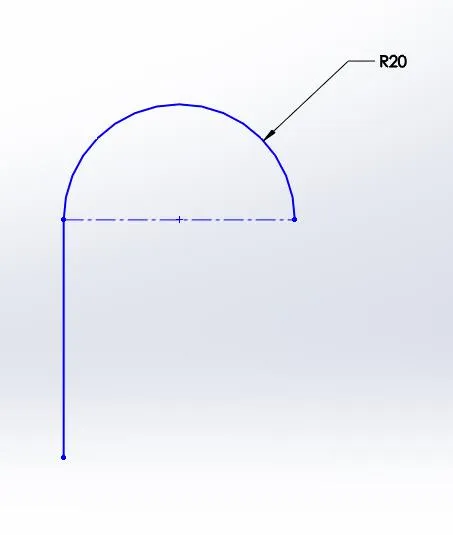
C-0 Continuité                                                                                                              Continuité      

Continuité de la courbure (C-2)

La continuité de courbure s'appuie sur les continuités C-0 et C-1, ce qui signifie qu'elle maintient la continuité de contact et la continuité de tangente, ainsi que la continuité de courbure. La section suivante abordera la définition de la courbure et de la courbure dans le contexte de notre exemple de ligne et d'arc.

Courbure

Intuitivement, le concept de courbure est probablement déjà compris. Prétendre que la région A de la spline illustrée ci-dessous est « plus courbée » que la région B ne susciterait guère de protestations.

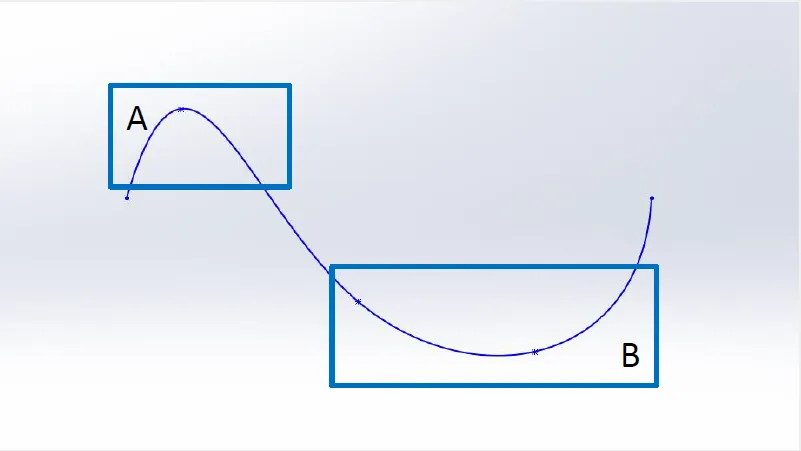
Spline avec différents degrés de courbure

Cependant, définir mathématiquement la courbure peut être moins évident. Si on veut l'analyser, une définition quantitative est nécessaire. Cette définition est en fait assez simple : la courbure (k) est égale à l'inverse du rayon (r).

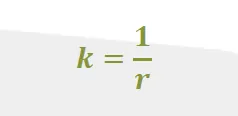
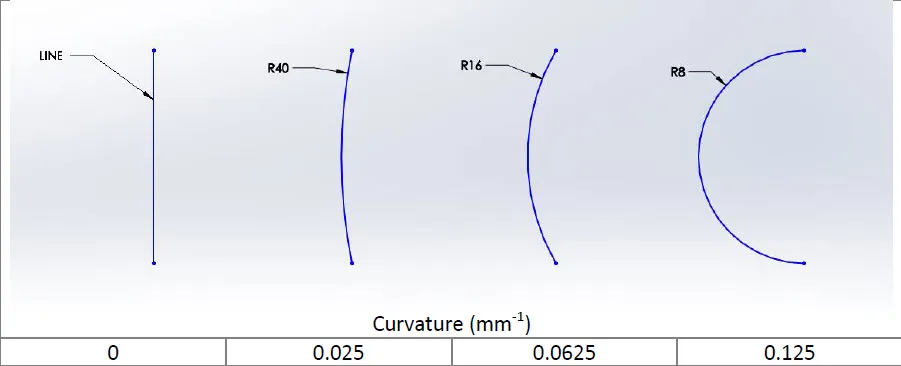
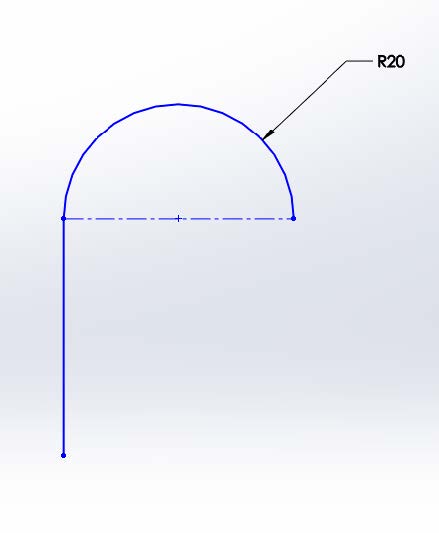
La relation inverse entre rayon et courbure peut être observée en observant un arc dont le rayon tend vers l'infini. Si l'on observe la figure ci-dessous de droite à gauche, le rayon tend vers l'infini. Simultanément, la courbure tend vers zéro. La ligne a une courbure nulle, ce qui est intuitivement logique, et son rayon est infini.

Assurer la continuité des courbures peut avoir un impact considérable sur l'apparence et le toucher d'un produit. Dans l'industrie automobile, on parle de « surfaçage de classe A ». Le maintien de la continuité C-2 améliore considérablement l'apparence du vernis sur la voiture. Il donne aussi aux produits grand public un toucher beaucoup plus lisse.

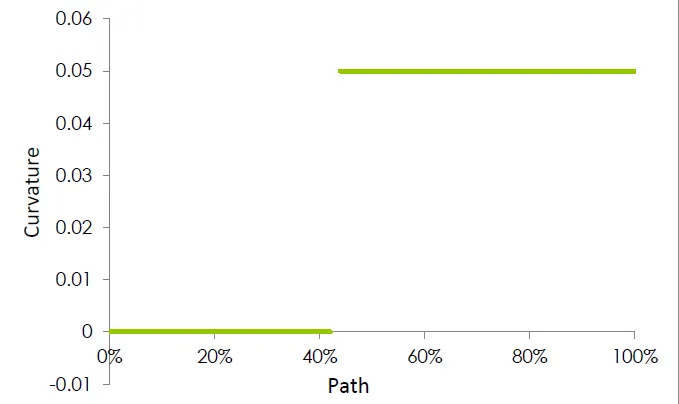
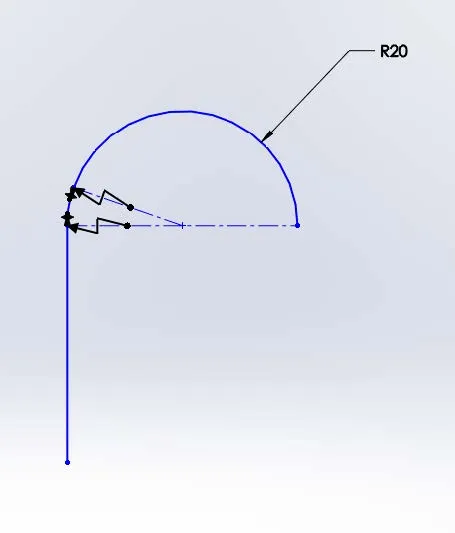
En reprenant notre exemple de ligne et d'arc, on constate que notre exemple C-1 ne peut pas assurer la continuité C-2. La ligne ayant une courbure constante de zéro et l'arc une courbure constante de 0,05 (rayon de 20), un graphique de la courbure le long du trajet montrera une discontinuité.

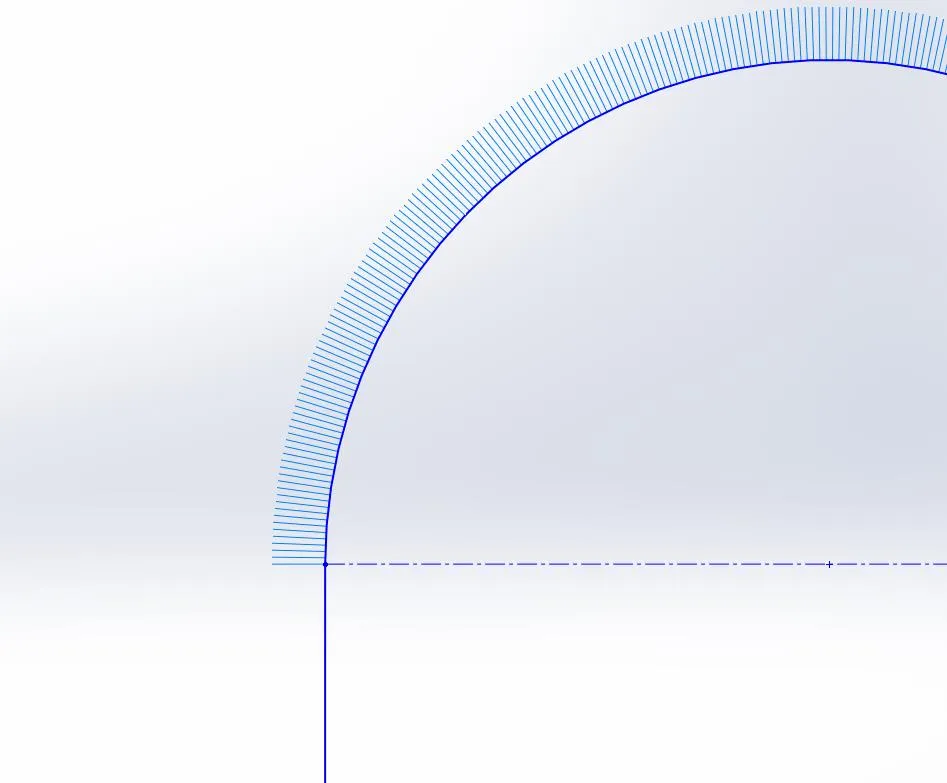
Croquis de lignes et d'arcs avec peignes de courbure

Pour combler cette lacune, nous utiliserons l'entité d'esquisse du début de notre discussion sur la courbure : la spline. Comme nous l'avons vu précédemment, une spline peut modifier sa courbure au sein d'une même entité d'esquisse. De plus, sa courbure est continue sur toute sa longueur. L'ajout d'une relation de courbure continue au sommet entre la ligne et la spline, puis entre la spline et l'arc, assurera une continuité C-2 à chaque sommet. (Remarque : la continuité C-2 peut également être obtenue en utilisant une spline ajustée.) L'esquisse et le graphique obtenus sont les suivants.

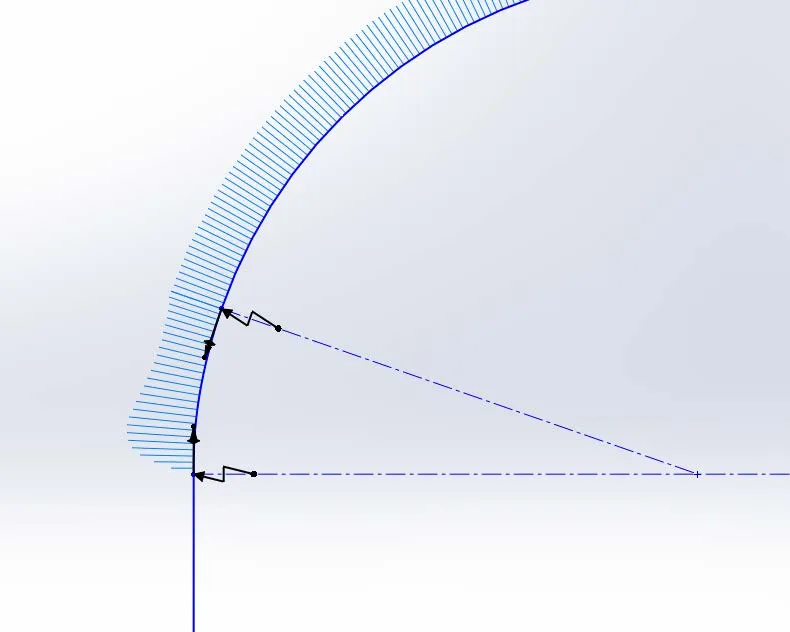
Spline comblant l'écart de courbure

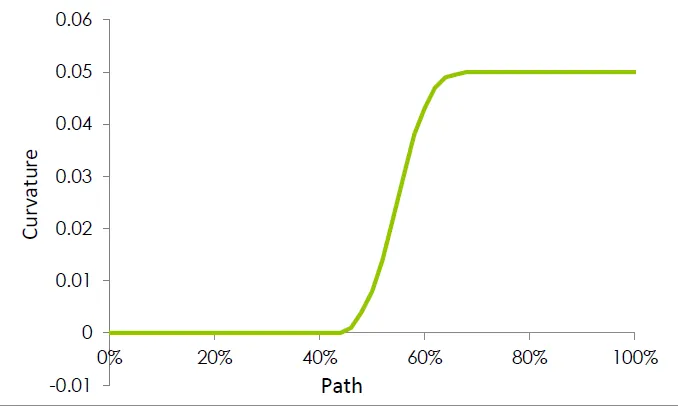
C-1 Continuité C-2 Continuité C-2 Continuité

Une fois l'esquisse de courbure continue obtenue, la fonction créée avec cette esquisse comportera des surfaces continues C-2, comme illustré ci-dessous. Dans Continuité et courbure de SOLIDWORKS (Partie 2), nous examinerons des exemples tridimensionnels de continuité C-0, C-1 et C-2 et les outils SOLIDWORKS que nous pouvons utiliser pour analyser la continuité et la courbure de nos modèles.

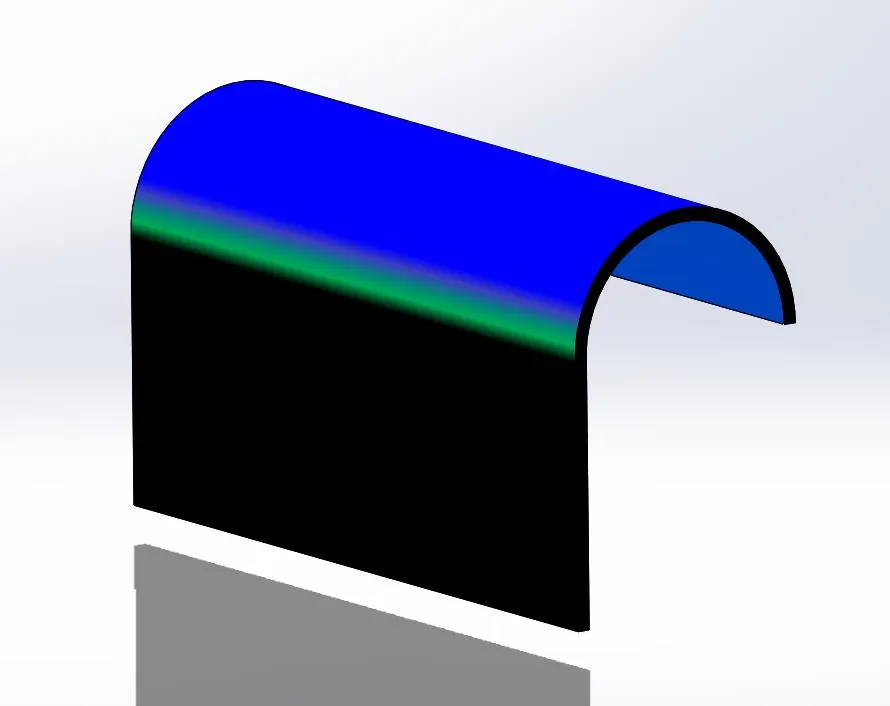
Extrusion de caractéristiques fines de notre esquisse avec affichage de la courbure activé

Nos derniers conseils et astuces SOLIDWORKS

Utilisation de la fonction Déplacer/Copier le corps dans SOLIDWORKS

Recherche de fonctions dans SOLIDWORKS 2021

Comment installer et dépanner les polices dans SOLIDWORKS

Vues de section personnalisées

Configuration de tolérance