Mathématiques et art des rouleaux lisses dans SOLIDWORKS

Patrick Roberts, passionné de géométrie et technicien dans une grande entreprise technologique, s'est vu offrir un casse-tête géométrique consistant à créer le solide lisse ultime. Grâce à son intelligence et à un peu de temps libre étalés sur deux semaines, il a imaginé l'un des solides lisses non sphériques les plus simples. Son article,ici, décrit le produit final et une preuve approximative de sa solidité mathématique. En juillet 2021, sa création a étévérifié par le travail de trois mathématiciens deUNAM.

Dans cet article, on va montrer les propriétés du tétraèdre de Roberts en utilisant SOLIDWORKSVous pouvez donc créer le vôtre de A à Z. Si vous préférez éviter le défi, nous avons mis à votre disposition une version à la fin de l'article. Vous pouvez la télécharger et l'imprimer pour l'afficher sur votre bureau ou la montrer à vos proches.

Solides de largeur constante

Pour créer un solide (autre qu'une sphère) qui roule en douceur entre les plans, vous devez créer une forme ayant une largeur constante.

Cela signifie que lorsque le solide est placé entre deux plans parallèles, il maintient toujours la même distance entre les plans, peu importe l'orientation. Un exemple de solide bidimensionnel, qui possède cette propriété, est appelé unTriangle de Reuleaux.

Le triangle de Reuleaux a plusieurs utilisations. Une application courante est le moteur Wankel. (Figure 1)

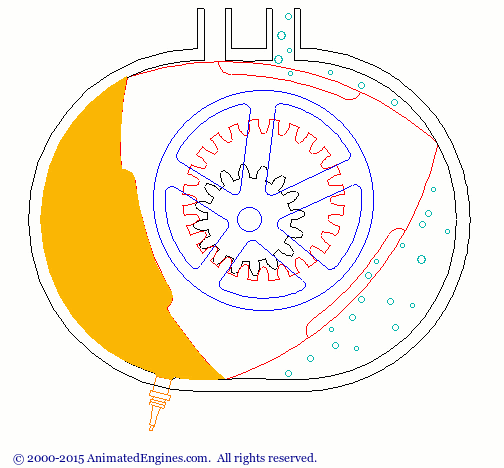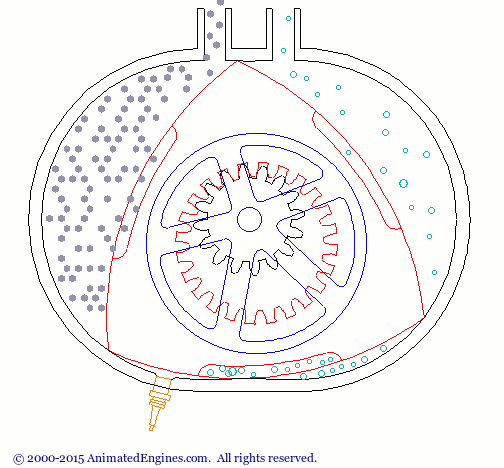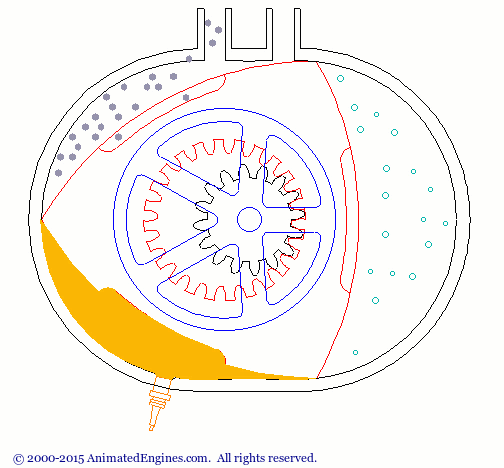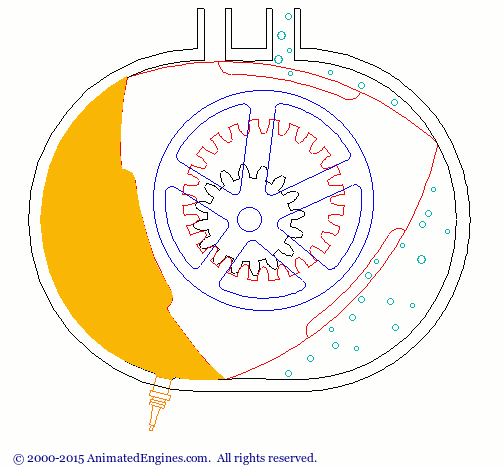
Figure 1 - Animation du moteur Wankel (source : http://animatedengines.com/wankel.html)

Ou il est utilisé par certains passionnés pour aider à percer des trous carrés comme le montre l'animation ci-dessous.

Figure 2 - Perçage de trou carré (source : https://youtu.be/L5AzbDJ7KYI )

Tétraèdre de Reuleaux

Pour construire notre propre tétraèdre de Roberts, on peut commencer par construire une forme proche de la largeur constante : le tétraèdre de Reuleaux. (Figure 3)

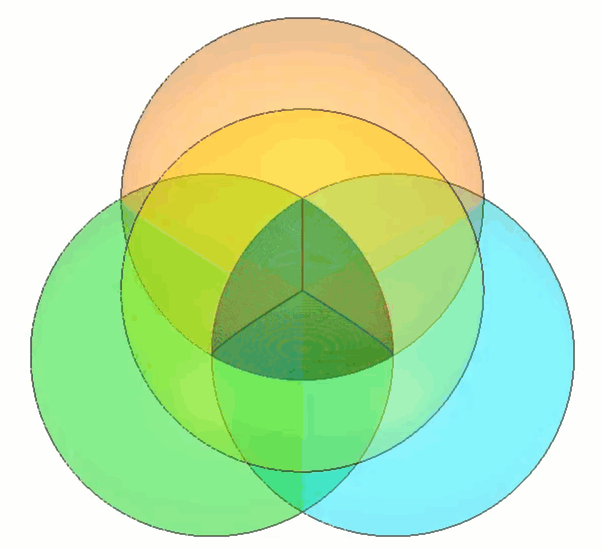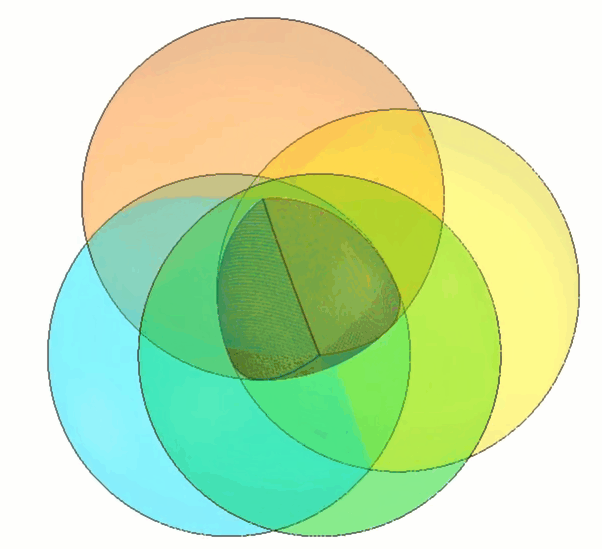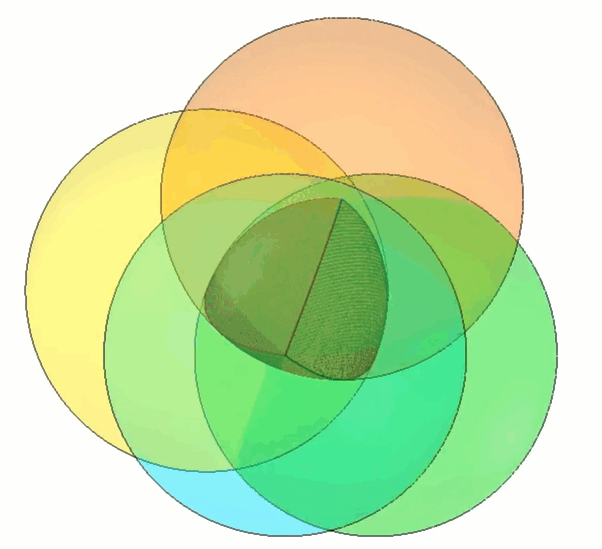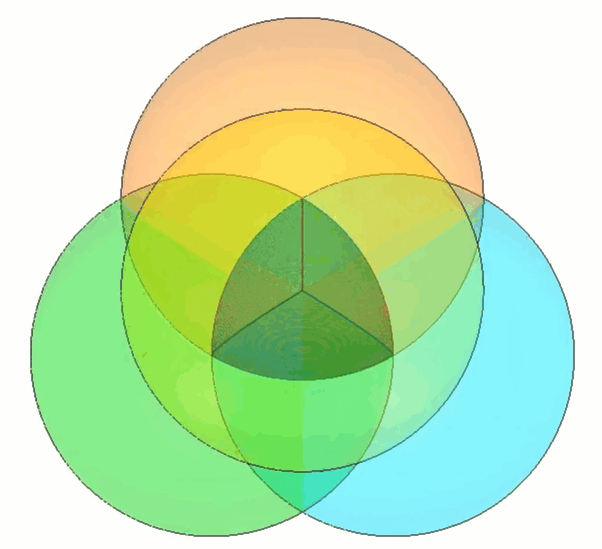
Figure 3 - Tétraèdre de Reuleaux représenté au milieu

La construction de ce tétraèdre est simple car elle implique la combinaison de quatre sphères espacées symétriquement au centre. (Figure 4)

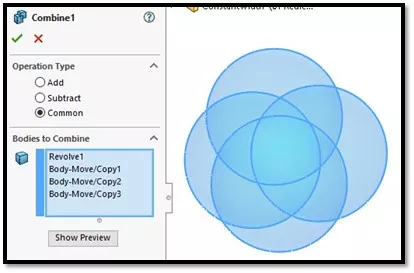
Figure 4 - Combiner commun

Peapod rond

Après avoir construit le tétraèdre de Reuleaux, l'étape suivante consiste à arrondir tous les coins, mais d'une manière particulière. (Figure 5)

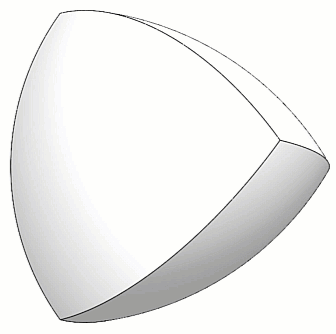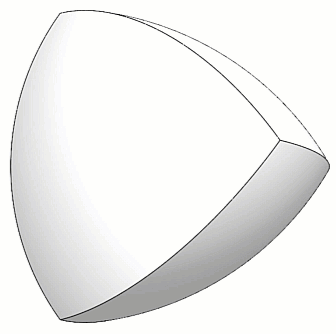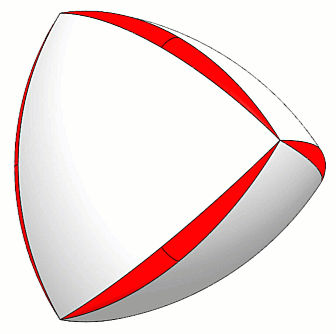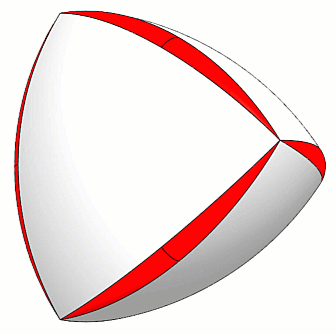
Figure 5 - Coins arrondis du Peapod

Comme décrit par les mathématiciens de l'UNAM, ce rond doit prendre la forme d'une cosse de pois où chaque « pois » (sphère) est tangent aux deux surfaces adjacentes et au bord du tétraèdre plat qui est intégré à l'intérieur du tétraèdre de Reuleaux. (Figure 6)

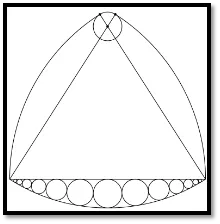
Figure 6 - Vue en coupe ronde d'une cosse de pois

Nous avons zoomé sur la cosse de pois ronde terminée pour que vous puissiez voir plus clairement à quoi elle ressemblera une fois les étapes suivantes terminées. (Figure 7)

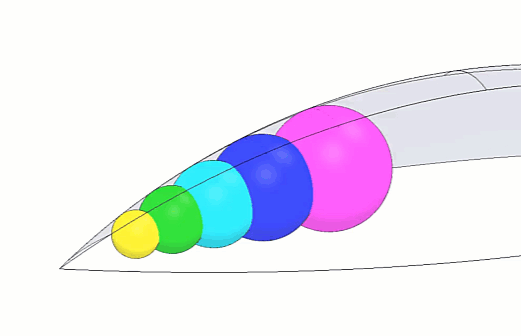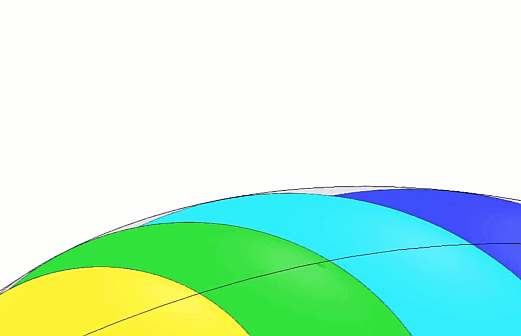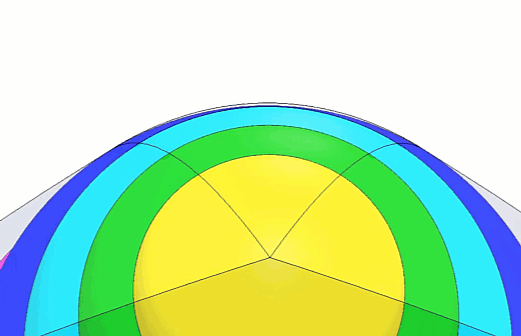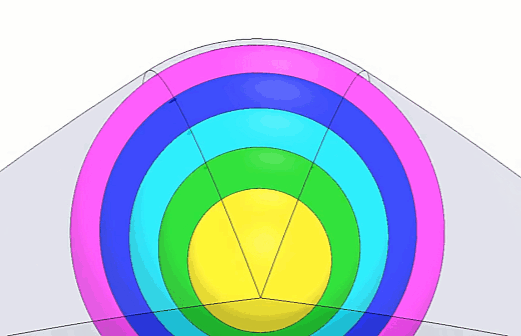
Figure 7 - Animation ronde de Peapod

Construction ronde Peapod

SOLIDWORKS n'a pas de fonctionnalité permettant de balayer une sphère à rayon variable. Pour créer la surface du rond en forme de cosse, on peut utiliser la commande Balayage de surface avec un cercle.Un chemin piloté par équation sera au centre du balayage et une courbe de guidage réduira le rayon à zéro à mesure qu'il approche des extrémités du chemin. (Figure 8)

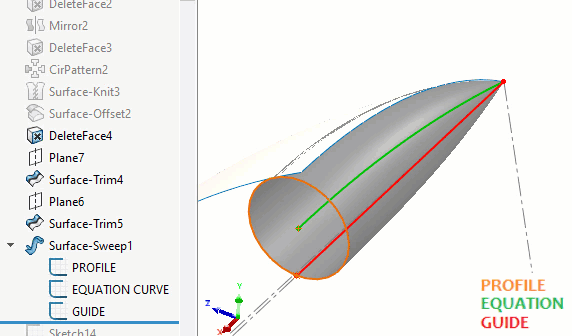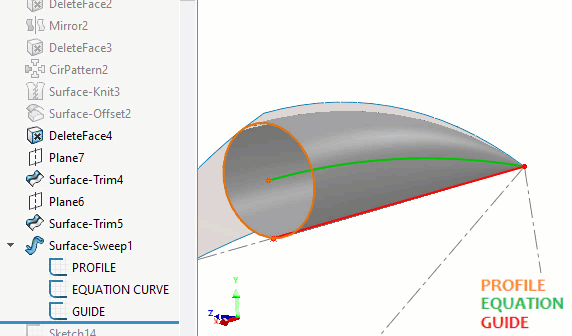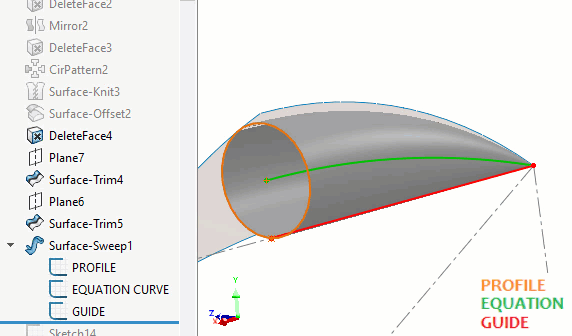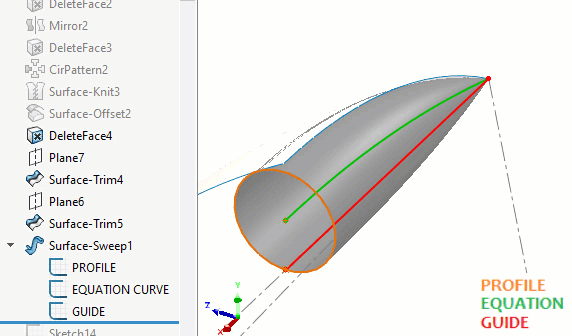
Figure 8 - Construction du balayage de surface d'un rond de cosse de pois

Nous avons d'abord construit le chemin à l'aide d'une courbe pilotée par équation. (Figure 9) Il s'agit d'une courbe décrivant l'emplacement du centre des sphères. L'équation correspondante est donnée dans l'article original de Roberts.

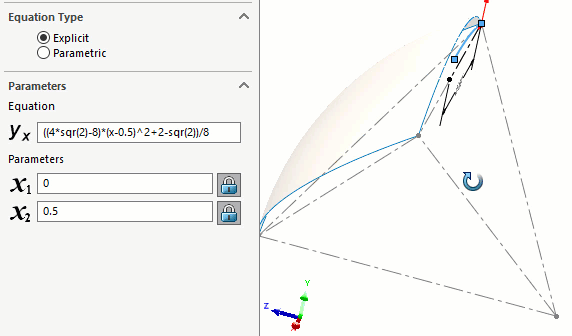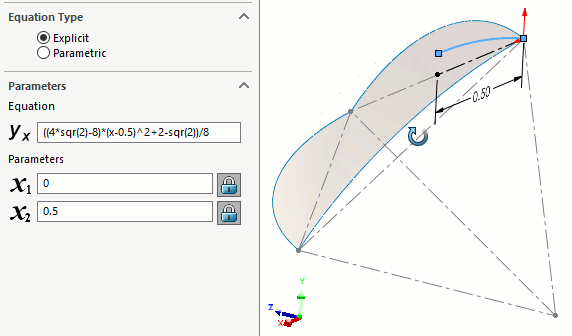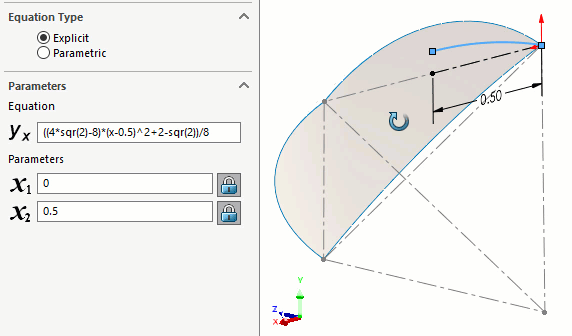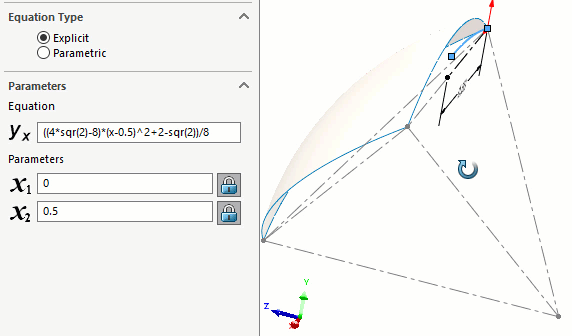
Figure 9 - Trajectoire centrale des sphères donnée par Roberts

Nous allons ensuite dessiner un profil circulaire qui suivra le chemin et restera normal à celui-ci.

Est-ce que l'utilisation d'un cercle au lieu d'une sphère fonctionnerait ?

La figure 7 (ci-dessus) devrait fournir une « preuve du concepteur » que le résultat devrait au moins être extrêmement proche (probablement dans les tolérances d’impression 3D) voire une correspondance exacte.

UN courbe de guidageIl faut déplacer le rayon de ce cercle le long de sa trajectoire. Ce guide est fourni par le bord droit du tétraèdre encastré. (Figure 10)

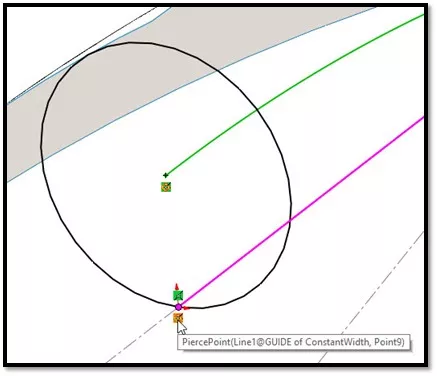
Figure 10 - Profil d'un balayage

Finalement, l'orientation du profil circulaire doitsuivre le cheminau lieu de rester dans une orientation constante pour imiter au mieux ce que ferait un balayage sphérique. (Figure 11)

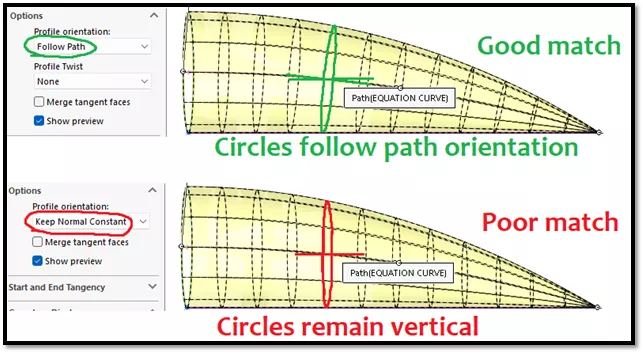
Figure 11 - L'orientation du profil circulaire doit suivre le chemin pour un résultat précis

Étonnamment, le balayage s'est terminé sans erreur même lorsque le rayon du cercle a diminué à zéro au sommet du tétraèdre.

Une fois la partie difficile terminée, il ne reste plus qu’à copier, refléter, modeler, découper et tricoter ces mêmes surfaces pour créer le tétraèdre de Roberts final.

Tétraèdre de Reuleaux contre tétraèdre de Roberts

Comment le tétraèdre de Roberts se compare-t-il à son cousin de largeur variable, le tétraèdre de Reuleaux ? On peut mettre en place un test virtuel à l'aide deSOLIDWORKS Motionet la différence est claire.

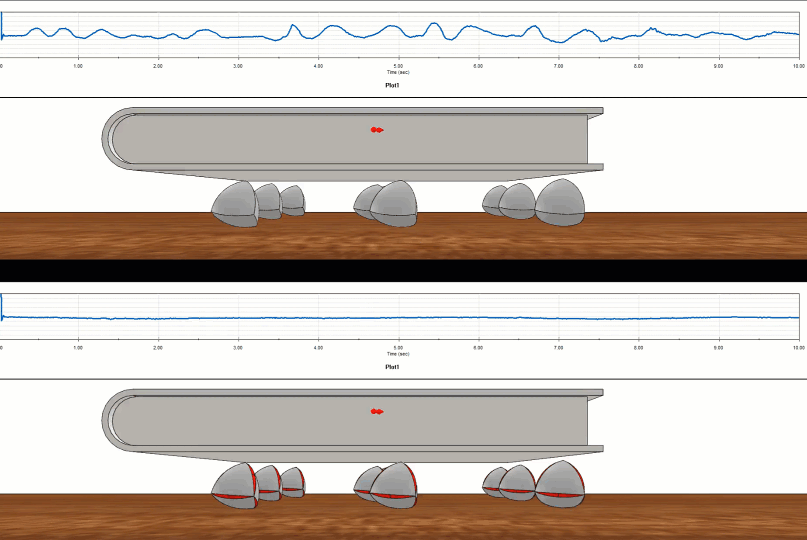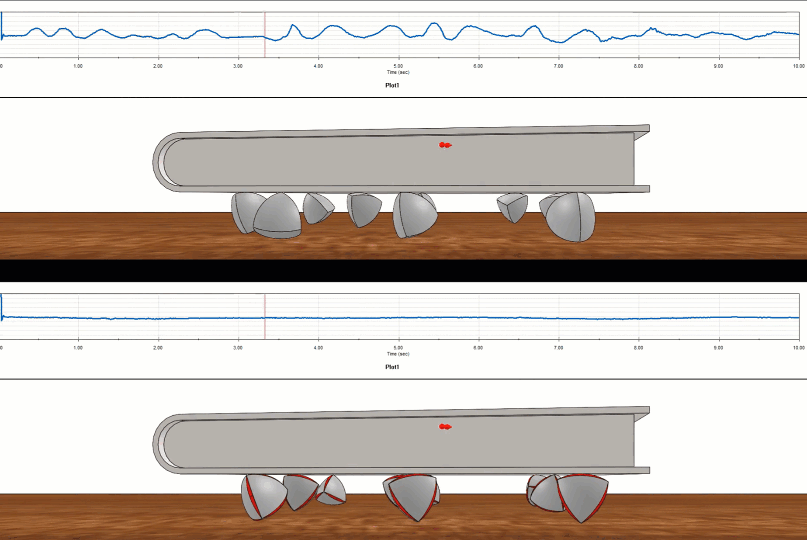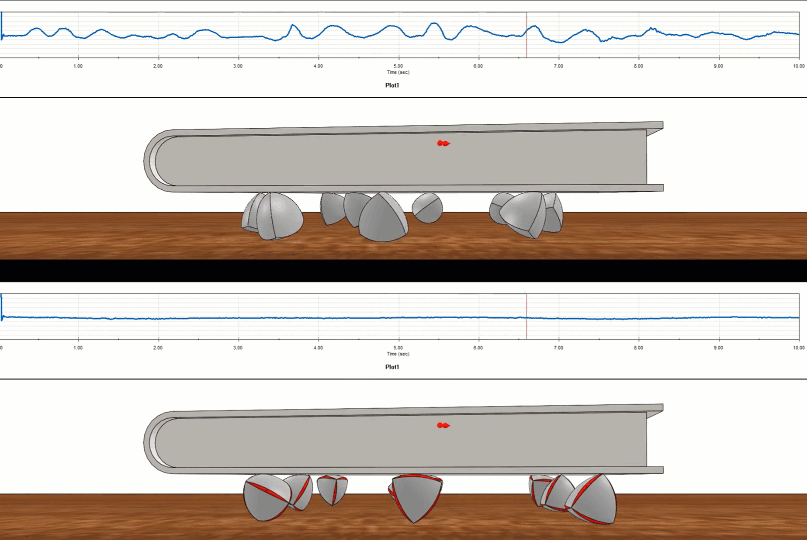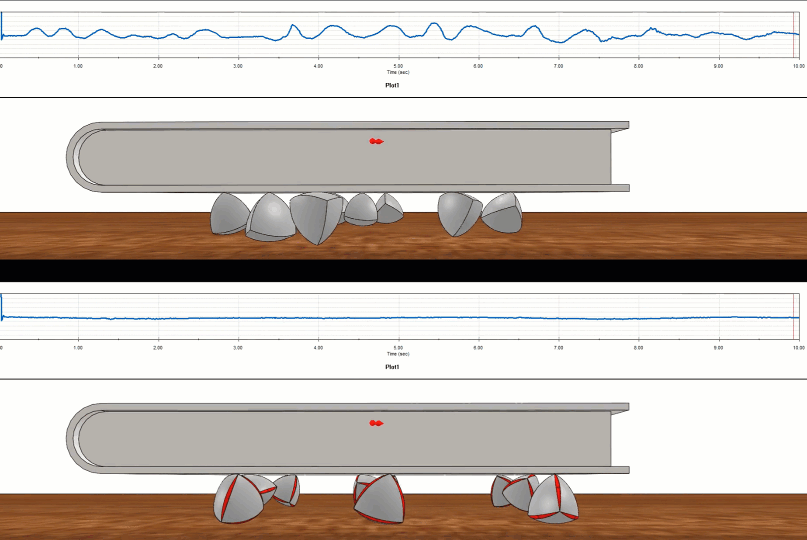
Figure 12 - Étude du mouvement SOLIDWORKS sur Reuleaux (en haut) par rapport à Roberts (en bas)

Le tétraèdre de Realeaux était un parcours cahoteux comparé au parcours fluide du tétraèdre de Roberts.

Finalement, nous avons testé une version imprimée en 3D.

Figure 13 - Tétraèdre de Roberts imprimé en 3D

Si je n'avais pas déjà su ce qu'il y avait sous le livre, j'aurais pensé qu'il était sur roulement à billes. Mais ne nous croyez pas sur parole, essayez d'imprimer le vôtre ! Téléchargement disponible ici.

Une version du Tétraèdre de Roberts convertie en dé à quatre faces a également été présentée sur la chaîne YouTube de Grand Illusions. Regardez leur vidéo.ici!

Résumé

La construction de cette forme d'apparence simple a nécessité des fonctionnalités SOLIDWORKS délicates et des idées créatives pour mettre au défi même les utilisateurs avancés.

1. Combiner commun
2. Spline pilotée par équation
3. Balayage avec une courbe de guidage
4. Motifs de surface, garnitures et tricot

Finalement, on a simulé la différence de comportement entre les deux conceptions à l'aide de SOLIDWORKS Motion pour vérifier les performances de notre conception améliorée.

Articles connexes

Comprendre la valve Tesla à l'aide de Simulation SOLIDWORKS

L'effet rétro est essentiel à vos lancers francs au basketball ! Une étude de simulation SOLIDWORKS

Comprendre le mystère du Rattleback avec SOLIDWORKS Motion

SOLIDWORKS Motion : un truc pour gérer les problèmes de performance

Nouveautés SOLIDWORKS 2022 : routage, systèmes structurels, pièces et fonctionnalités

VOIR TOUS LES ARTICLES SOLIDWORKS