Conseils de maillage Abaqus pour des résultats de stress précis
Des résultats de contrainte fiables sont essentiels pour prendre des décisions d'ingénierie éclairées, assurer la sécurité et optimiser les conceptions. Lors d'une simulation, il est essentiel que les résultats soient conformes aux observations réelles, malgré les hypothèses et les approximations présentes dans toute analyse. Atteindre la précision Abaqus il ne s’agit pas seulement de créer votre modèle et de cliquer sur le bouton « Exécuter ».
Une modélisation et une configuration analytiques rigoureuses sont nécessaires pour éviter les erreurs et les résultats trompeurs. Un maillage suffisamment raffiné, avec des choix d'éléments appropriés, est le meilleur moyen d'équilibrer efficacité et précision des résultats d'analyse. Ce blogue explore les principales techniques de maillage permettant d'améliorer la précision et la fiabilité des résultats de contrainte dans Abaqus.
Sélection du type d'élément
Choisir le bon type d'élément est la première étape cruciale de la génération de maillage. Faut-il utiliser des éléments solides (3D), des coques (2D) ou des poutres (1D), ou une combinaison des deux ?
Si l'objectif est la précision, les éléments solides peuvent sembler évidents. Après tout, le monde réel est tridimensionnel ; ne devrait-on pas utiliser des éléments tridimensionnels pour refléter cela, plutôt que des simplifications ?
En réalité, les tests montrent que les éléments de coque ou de poutre, lorsqu'ils sont bien choisis, fournissent des résultats précis tout en économisant les ressources de calcul. En général :
- Le maillage en coque est utile pour les corps minces d'épaisseur uniforme (tôle, etc.)
- Le maillage de poutres est particulièrement adapté – vous l’avez deviné – aux poutres (et aux fermes), en particulier lorsque la longueur de la poutre est au moins dix fois supérieure à son diamètre transversal.
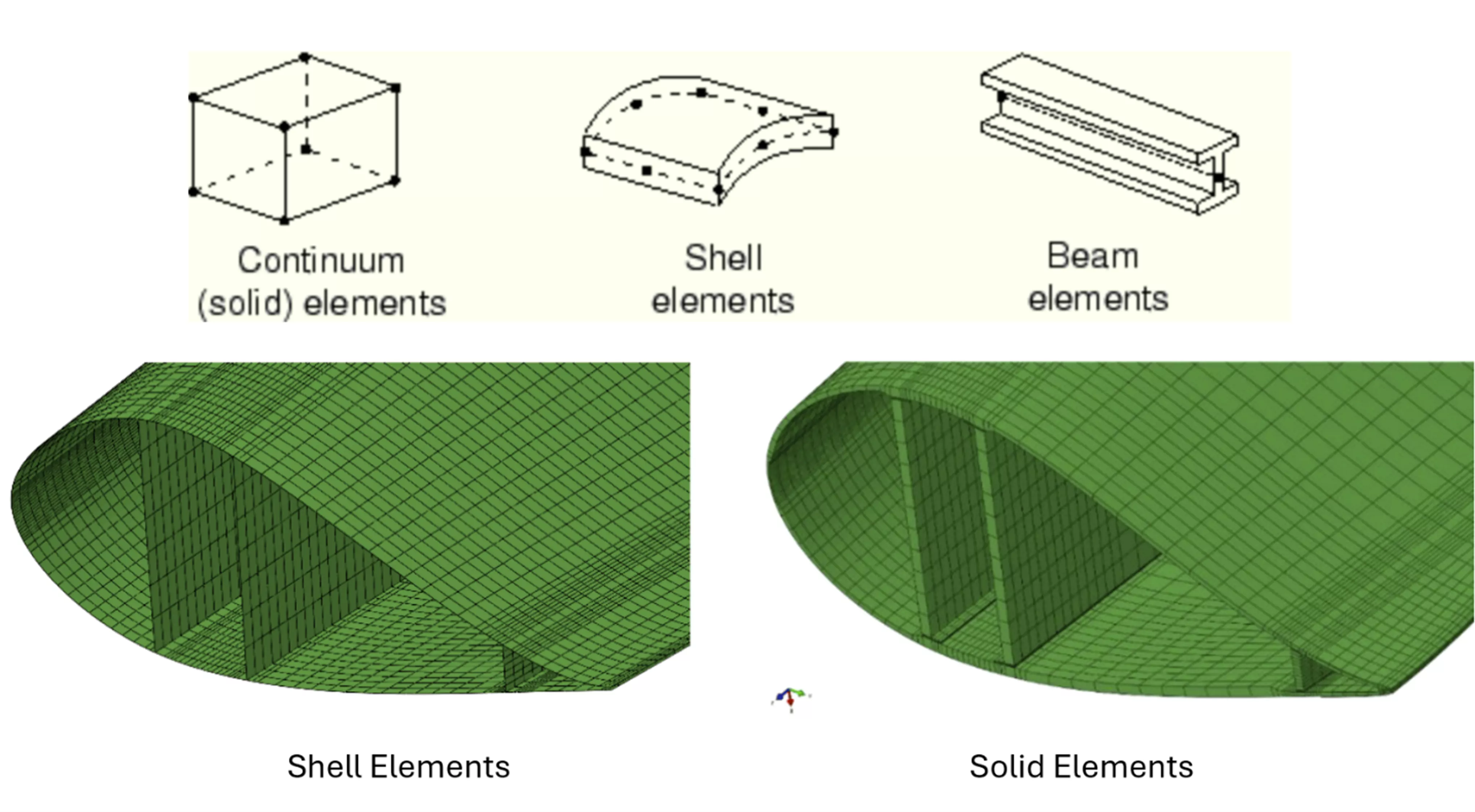
Figure 1 : Exemple d'éléments solides, coques et poutres
Supposons que vous ayez besoin de calculer la déviation à l'extrémité d'une poutre en porte-à-faux de 1,5 m (section carrée 0,05 m x 0,05 m) sous une charge uniforme de 200 N/m :
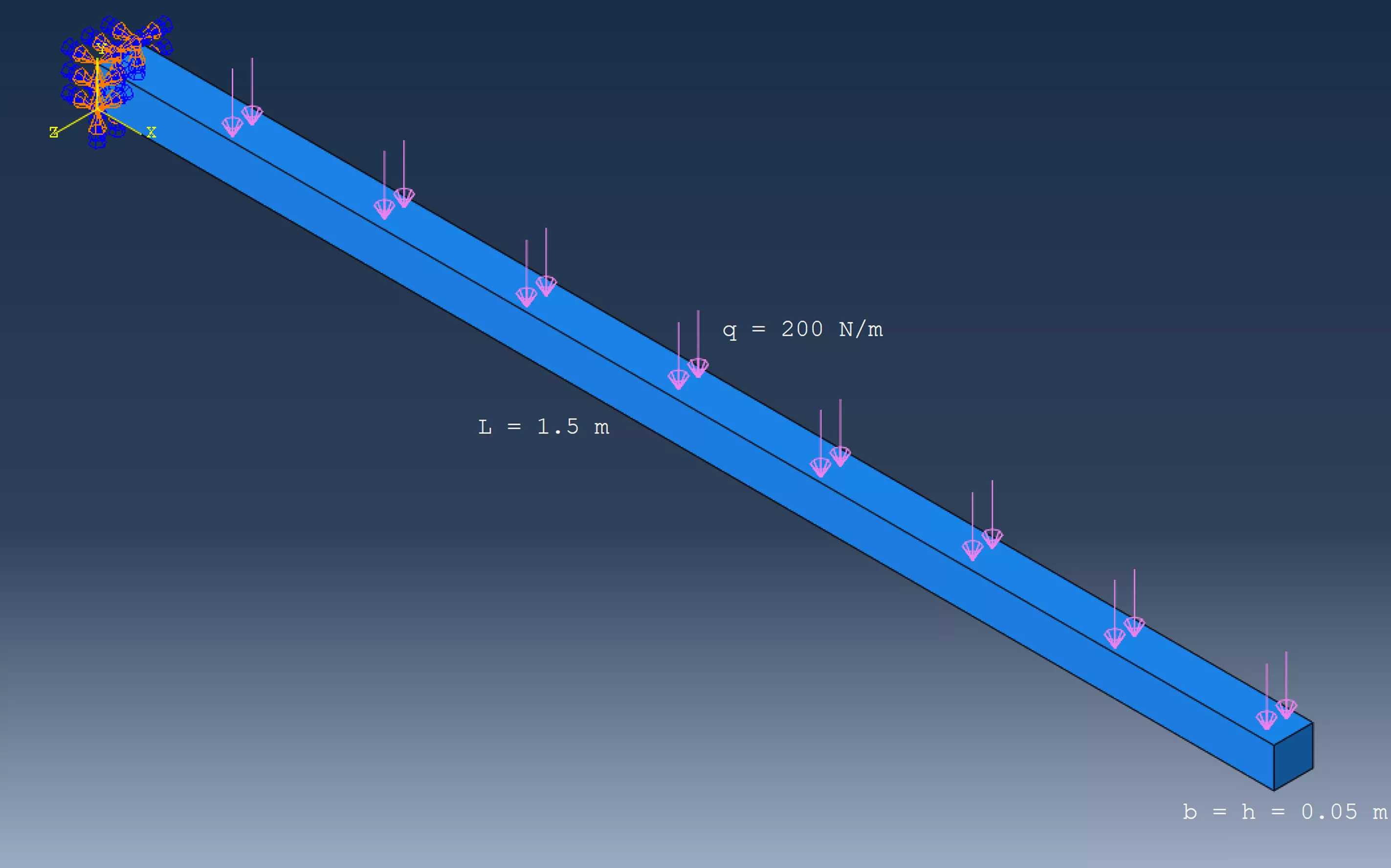
Figure 2 : Configuration du problème de poutre en porte-à-faux
Faisons le calcul...
Déflexion maximale (δ) = (qL4)/(8e)
- q= force appliquée = 200N/m
- L= longueur du faisceau = 1,5 m
- E= module d'élasticité = 50moyenne générale
- Je= moment d'inertie = (1/12)b4= (1/12)(0,05)4= 5,208333e–7 m4
δ = (200 * 1,54) / (8 * 50e9 * 5.208333e–7)
= 0,004860m
= 4.860mm
Les mathématiques nous disent que la déflexion maximale est 4 860 mmSi je modélise cela dans Abaqus et que je le maille avec des éléments solides, voici les résultats à différentes tailles de maillage :
| Taille de l'élément solide | Nombre d'éléments | Déflexion maximale | Erreur de calcul |
| 0,05 m | 30 | 5 880 mm | 20,99 % |
| 0,025 m | 240 | 4 774 mm | 1,77 % |
| 0,01 m | 3 750 | 4 829 mm | 0,64 % |
| 0,005 m | 30 000 | 4 846 mm | 0,29 % |
Figure 3 : Tableau des résultats lors de l'utilisation d'éléments solides
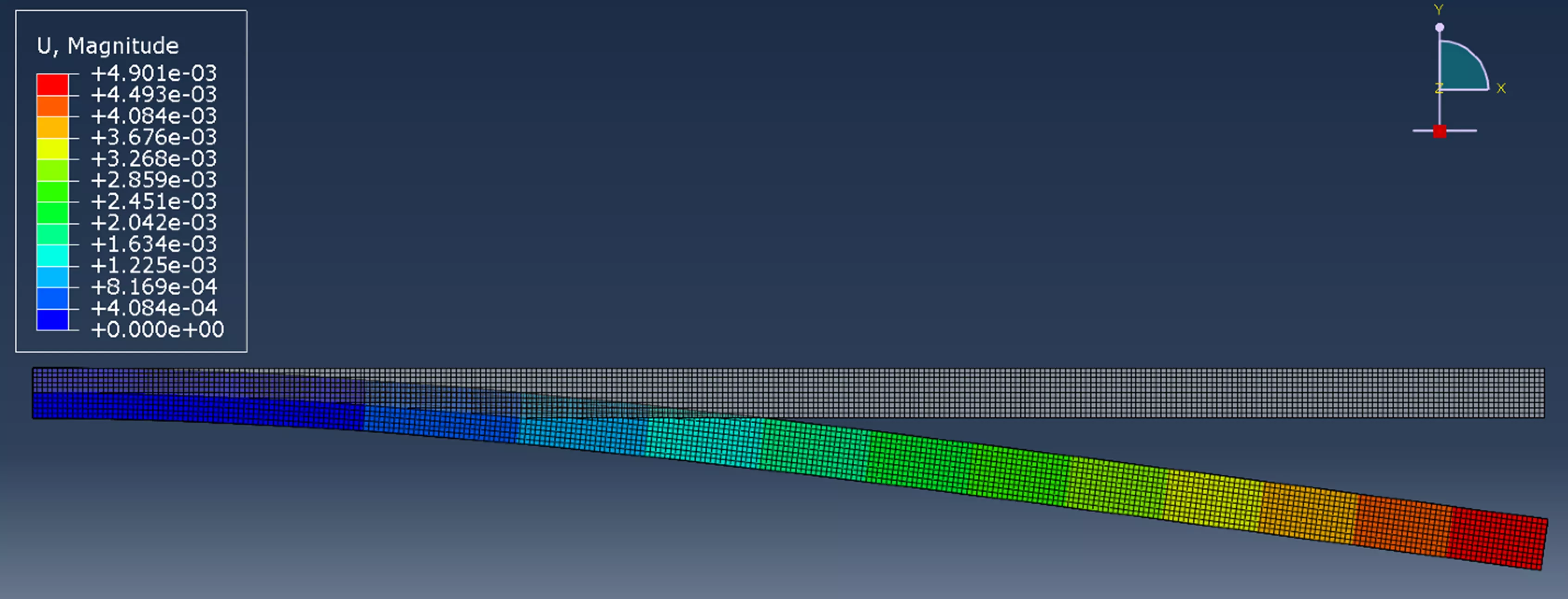
Figure 4 : Résultats de la déviation du faisceau
Si ce même modèle est maillé avec des éléments poutre, voici les résultats :
| Taille de l'élément de poutre | Nombre d'éléments | Déflexion maximale | Erreur de calcul |
| 0,05 m | 30 | 4 867 mm | 0,14 % |
| 0,025 m | 60 | 4 866 mm | 0,12 % |
| 0,01 m | 150 | 4 866 mm | 0,12 % |
| 0,005 m | 300 | 4 866 mm | 0,12 % |
Figure 5 : Tableau des résultats lors de l'utilisation d'éléments de poutre
Ainsi, bien que les éléments solides soient tridimensionnels et donc la représentation la plus proche du monde réel, un maillage très fin est nécessaire pour approcher la réponse calculée : environ 3 000 éléments sont nécessaires pour obtenir une erreur inférieure à 1 %. Comparez cela aux résultats du faisceau : avec seulement 30 éléments, ma réponse se situe déjà à 0,14 % de la valeur calculée.
Une idée semblable peut être appliquée au maillage de coque. Lorsqu'il est approprié, le maillage de coque peut être au moins aussi précis que le maillage solide tout en économisant de précieuses ressources de calcul. Tenez toujours compte de la forme des corps analysés et choisissez un type d'élément approprié.
Qualité des éléments et formulation/intégration
Une fois le type d'élément sélectionné, le choix suivant se fait entre les éléments du premier ordre (linéaires) et du second ordre (quadratiques), qui définissent la résolution et la qualité de chaque élément, suivis du type d'intégration de l'élément.
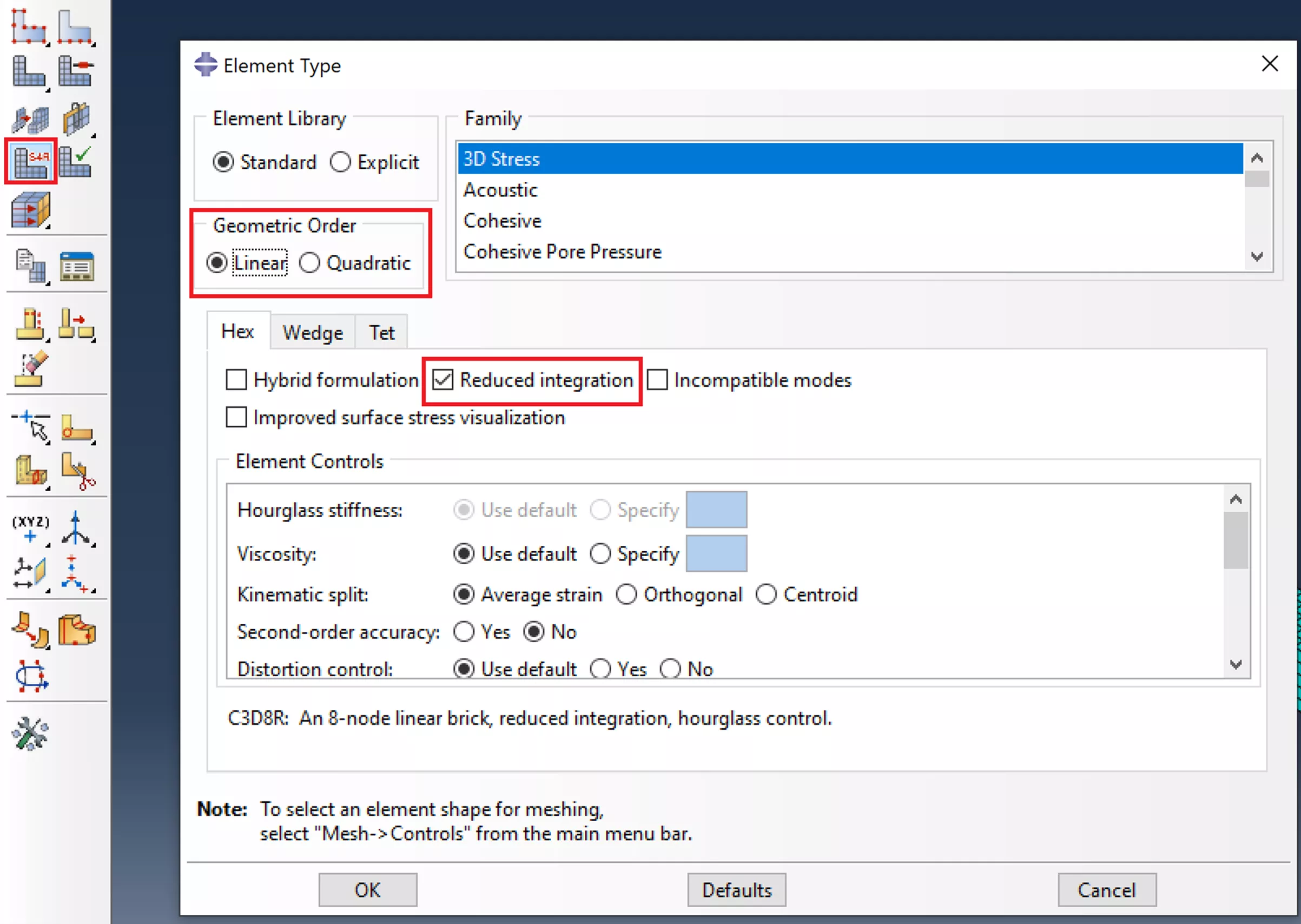
Figure 6 : Boîte de dialogue « Attribuer le type d'élément », où l'intégration et l'ordre sont choisis
Éléments de premier ordre et de second ordre dans l'analyse par éléments finis
Les éléments du premier ordre ont des nœuds à chaque coin, tandis que les éléments du second ordre ont des nœuds supplémentaires au milieu de chaque côté.
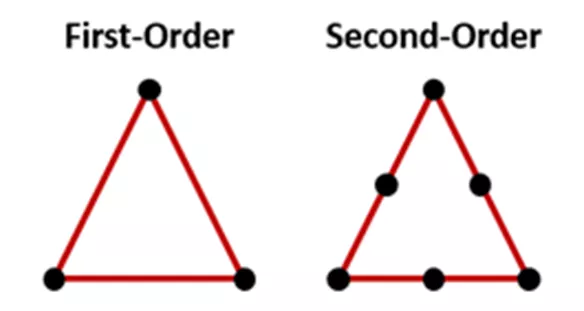
Figure 7 : La différence entre les éléments du premier et du deuxième ordre
Les nœuds supplémentaires des éléments de second ordre introduisent des degrés de liberté supplémentaires, ce qui entraîne une rigidité moindre et une déflexion plus précise que les éléments de premier ordre, plus rigides. Cependant, des articles de meilleure qualité impliquent un coût de calcul plus élevé et donc des temps de résolution plus longs. Dans certains scénarios, notamment les situations dynamiques à grande vitesse comme un accident de voiture ou un essai de chute, les éléments de premier ordre constituent le choix le plus stable.
Un autre point clé à considérer est la formulation et l'intégration des éléments. Voici les options d'intégration possibles :
- Intégration complète calcule le déplacement à tous les points d'intégration, appelés « points de Gauss », de chaque élément (par exemple, les éléments C3D8).
- Intégration réduite (comme les éléments C3D8R) calcule le déplacement en fonction d'un point de Gauss central pour chaque élément.
- Intégration sélective réduite (comme C3D8I) est une combinaison des deux : les éléments dans les zones de préoccupation (par exemple, cisaillement élevé ou contrainte volumétrique) seront entièrement intégrés à tous les points de Gauss, tandis que les éléments ailleurs utiliseront une intégration réduite.
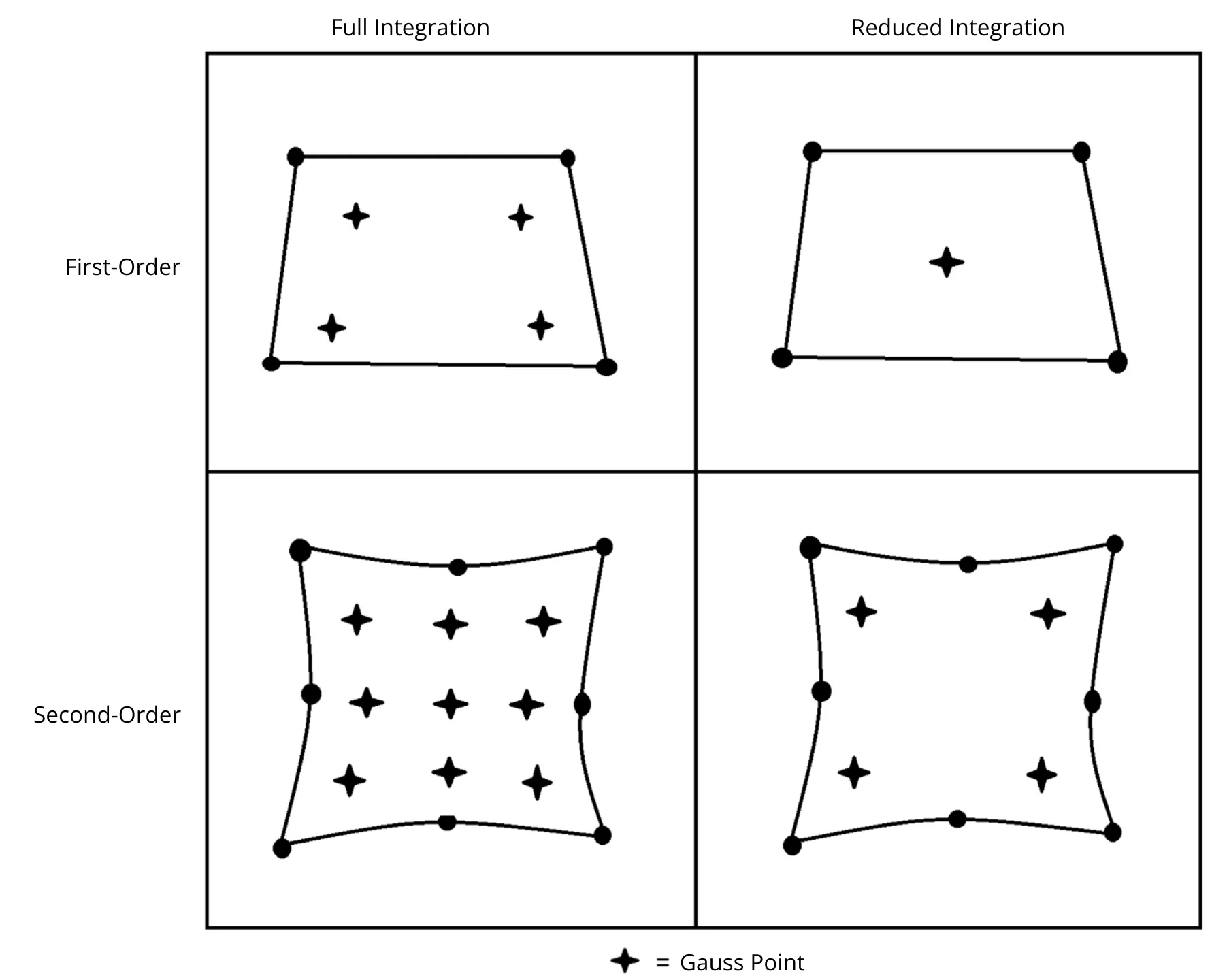
Figure 8 : La différence entre les types d'intégration des éléments
Comme pour la plupart des choix à faire lors de la mise en place d’un modèle d’analyse, chaque option comporte des avantages et des inconvénients qui doivent être équilibrés pour maximiser la précision et l’efficacité :
| Type d'intégration | Avantages | Inconvénients |
| Plein |
|
|
| Réduit |
|
|
| Sélectif réduit |
|
|
Figure 9 : Liste des avantages et des inconvénients de l'intégration complète, réduite et sélective réduite
Pour revenir à mon exemple de poutre en porte-à-faux, j'ai maillé et résolu l'étude avec quatre formulations d'éléments différentes : intégration complète du premier ordre, intégration complète du second ordre, intégration réduite du premier ordre et intégration réduite du second ordre. Voici un tableau des résultats :
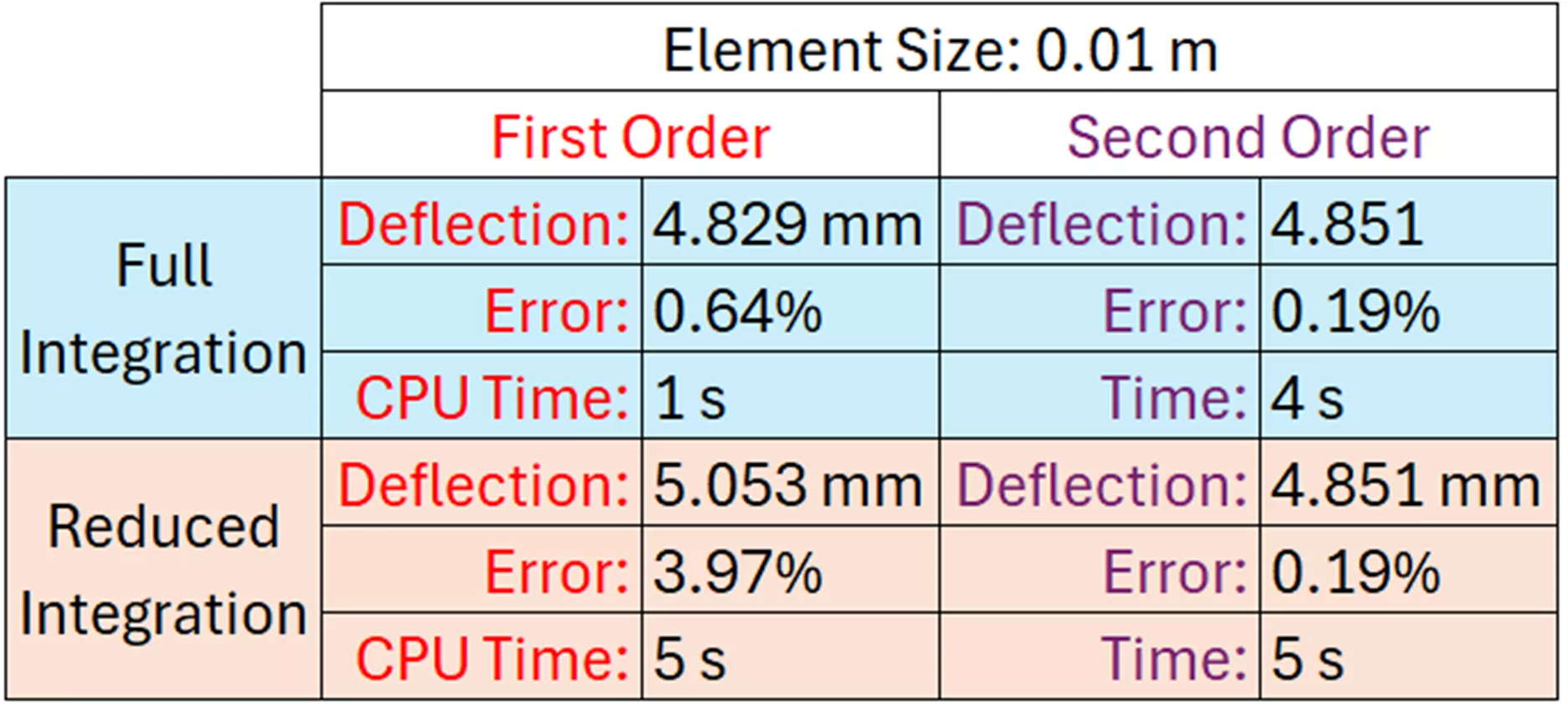
Figure 10 : Résultats comparant l'ordre des éléments et l'intégration dans le problème des poutres en porte-à-faux
Pour ce type de problème simple, il est évident que le temps de résolution n'est pas un problème majeur. Cependant, la précision varie considérablement selon la formulation choisie. La meilleure option est clairement l'intégration complète du second ordre, qui donne des résultats très proches de la réponse calculée de 4,860 mm, sans nécessiter de raffinement supplémentaire du maillage.
Le tableau suivant énumère une variété de types d'analyse avec leurs choix de qualité d'élément et de formulation recommandés :
| Type de problème | Type d'élément recommandé |
| Flexion (sans contact) |
Intégration complète du second ordre |
| Concentration de stress |
Intégration complète du second ordre |
| Fréquence naturelle (dynamique linéaire) | Intégration complète du second ordre |
| Géométrie de modèle complexe (matériau linéaire, sans contact) |
Hexaédrique du second ordre (si non déformé), tétraédrique du second ordre (si difficultés de maillage) |
| Géométrie de modèle compliquée (problème non linéaire ou contact) |
Hexaédrique du premier ordre (si non déformé), tétraédrique du second ordre (si difficultés de maillage) |
| Presque incompressible (v > 0,475) |
Intégration réduite du premier ou du second ordre |
| Complètement incompressible (v = 0,5) |
Hybride (premier ordre si de grandes déformations sont attendues) |
| Formage de métaux en vrac (forte distorsion de maille) |
Intégration réduite du premier ordre |
| Contact avec flexion |
Intégration réduite du premier ordre |
| Dynamique non linéaire (impact) |
Intégration complète du premier ordre |
| Contact entre corps déformables |
Intégration complète du premier ordre |
Figure 11 : Types d’éléments recommandés pour différents types de problèmes
Plus: Formulation et intégration d'éléments - Assistance utilisateur SIMULIA 2024
Contrôles de qualité du maillage
Une fois le type de maillage sélectionné, il est prêt à être généré. Il faut ensuite vérifier sa qualité. Un maillage déformé, biaisé ou excessivement incliné peut entraîner des erreurs de calcul ; il est donc important de les identifier et de les minimiser.
Vous pouvez accéder à l'outil de vérification de maillage d'Abaqus en passant au module Mesh et en allant dans Engrener > VérifierCet outil détecte et met en évidence les éléments de votre maillage qui ne répondent pas aux critères d'angles, de rapport hauteur/largeur, de longueur des arêtes, etc. Ces critères peuvent être définis par l'utilisateur, mais les valeurs par défaut sont généralement suffisantes.
Les zones problématiques rencontrées avec cet outil peuvent être résolues par un raffinement supplémentaire du maillage via des contrôles globaux ou locaux. Des éléments de plus petite taille permettent de réduire la distorsion et les proportions.
Plus: Vérification de votre maillage - Assistance SIMULIA 2024
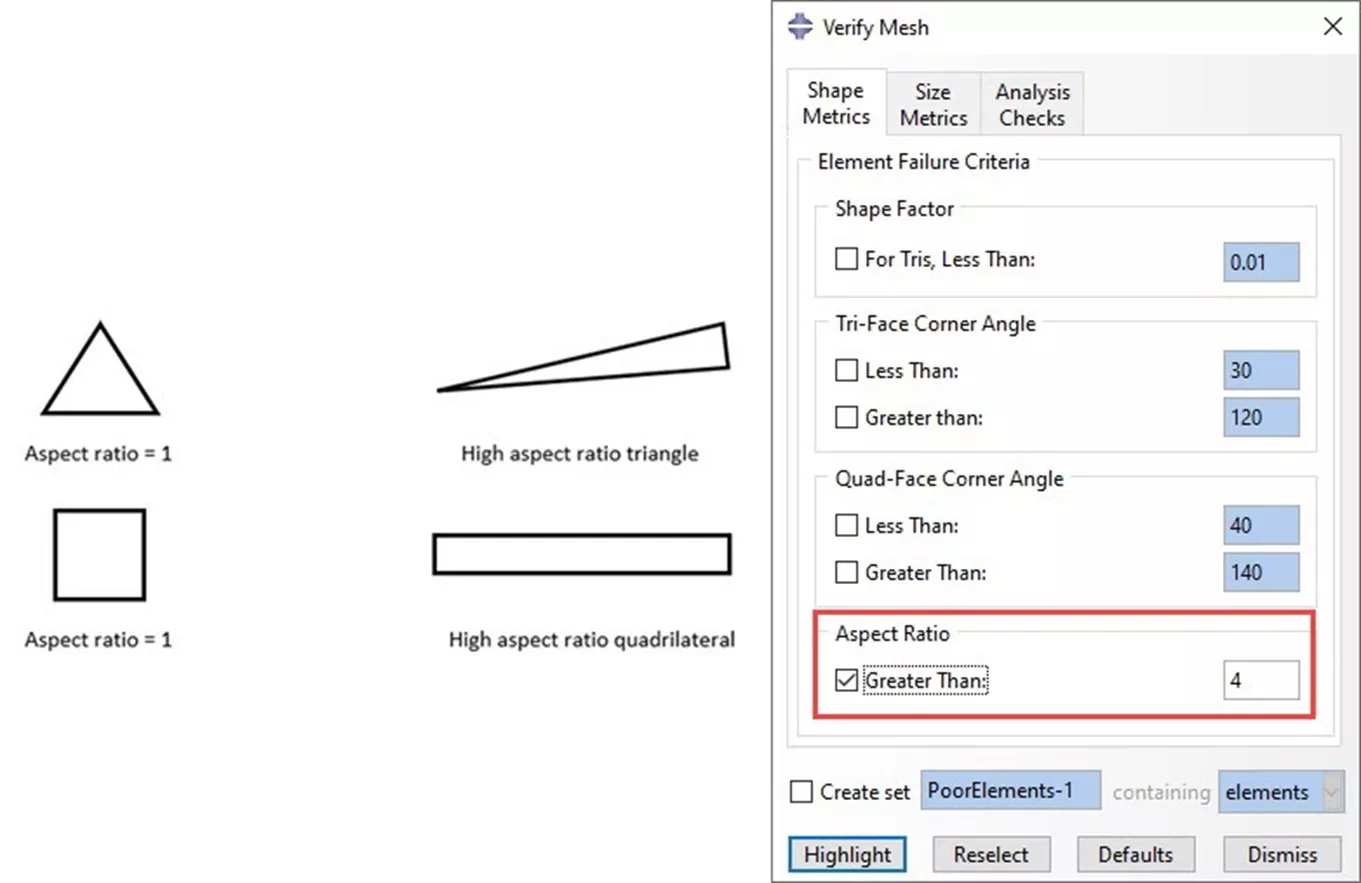
Figure 12 : Rapports d'aspect des éléments et comment vérifier la qualité du maillage
Analyse de sensibilité du maillage
Même après avoir créé et vérifié un maillage de haute qualité, il est risqué de se fier aveuglément aux résultats sans vérifier la convergence. Une analyse de sensibilité du maillage consiste à exécuter la simulation avec des maillages progressivement affinés pour voir à quel moment les résultats se stabilisent.
Reprenons par exemple l'exemple de poutre en porte-à-faux présenté précédemment. On constate qu'un raffinement du maillage était nécessaire pour approcher la réponse théorique de 4,860 mm. Cependant, à un certain stade, un raffinement supplémentaire n'améliore pas significativement les résultats et ne fait que ralentir le calcul.
| Taille de l'élément solide | Nombre d'éléments | Déflexion maximale | Erreur de calcul |
| 0,05 m | 30 | 5 880 mm | 20,99 % |
| 0,025 m | 240 | 4 774 mm | 1,77 % |
| 0,01 m | 3 750 | 4 829 mm | 0,64 % |
| 0,005 m | 30 000 | 4 846 mm | 0,29 % |
| 0,0025 m | 240 000 | 4 851 mm | 0,19 % |
Figure 13 : Résultats pour des tailles d'éléments décroissantes
Si vous commencez avec un maillage grossier, puis peaufinez jusqu'à ce que les résultats convergent, vous pouvez être sûr que votre résultat est un calcul précis du problème que nous avons mis en place.
Plus: Analyse de sensibilité de conception pour poutre en porte-à-faux - Soutien utilisateur SIMULIA 2024
Cependant, il existe quelques autres façons d'optimiser votre maillage pour qu'il fonctionne le plus efficacement possible, sans sacrifier la précision.
Sous-modélisation, maillage adaptatif et contrôle local du maillage
Avec un maillage suffisamment raffiné, composé d'un type d'élément et d'une formulation bien choisis, nous sommes sur la bonne voie pour générer des résultats fiables dans Abaqus. Cependant, optimiser le maillage et donner à votre ordinateur toute sa capacité de traitement n'est peut-être pas la technique la plus efficace pour obtenir les réponses dont vous avez besoin à partir d'une analyse.
Sous-modélisation
Sous-modélisation Il s'agit d'une technique permettant de concentrer le raffinement du maillage sur les zones d'intérêt sans avoir à affiner l'ensemble du maillage du modèle. Cela permet d'obtenir des résultats précis là où c'est nécessaire, sans forcer votre système à effectuer des calculs inutilement précis ailleurs.
Lors de la sous-modélisation, vous commencez par un maillage global grossier du modèle complet afin de capturer le comportement structurel global, qui est ensuite enregistré sous forme de résultats nodaux. Vous effectuez ensuite une analyse sur une région plus petite du modèle (appelée sous-modèle) avec un maillage fin, en appliquant les conditions aux limites de déplacement/contrainte héritées du modèle global grossier.
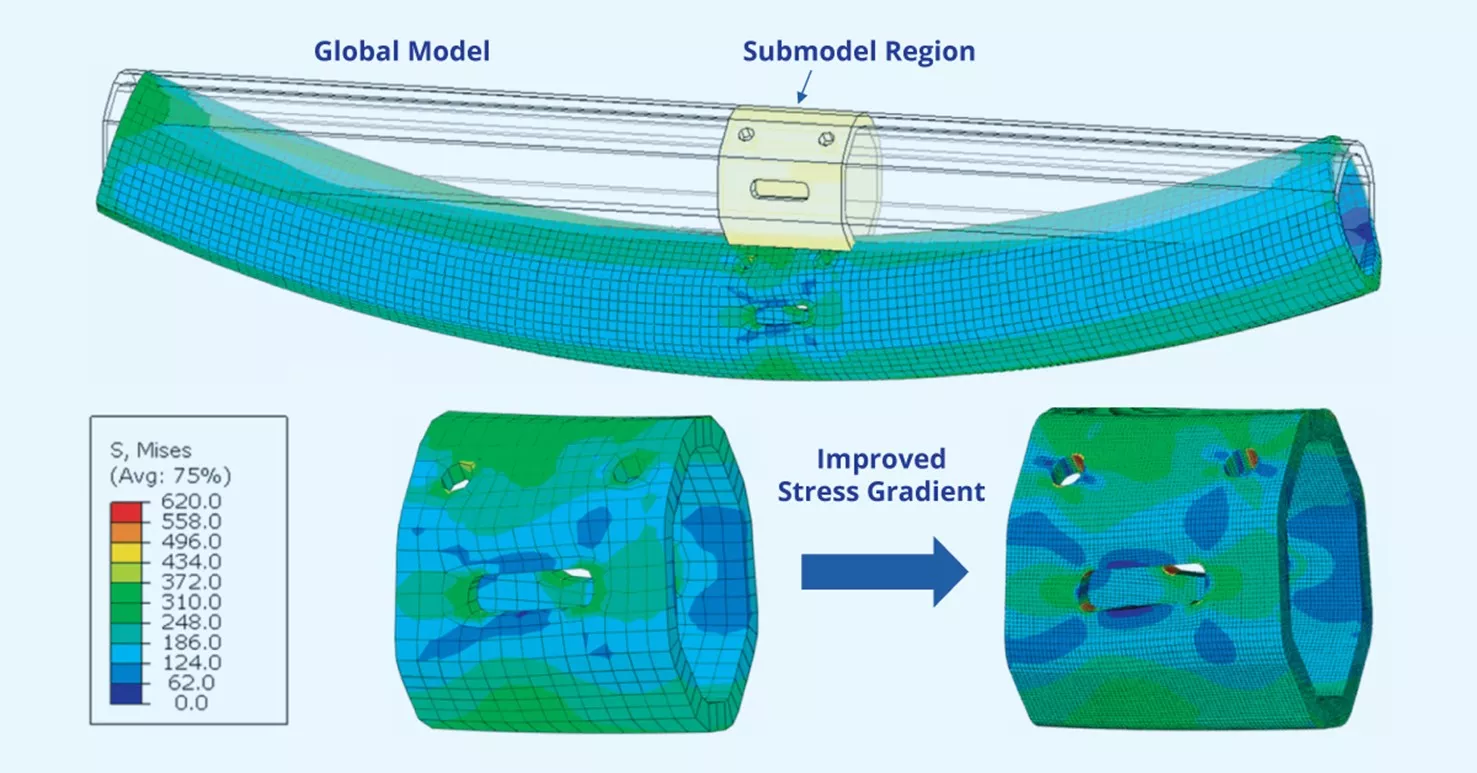
Figure 14 : Technique de sous-modélisation
Cette approche en plusieurs étapes est un excellent moyen de gérer de grands modèles contenant des zones de préoccupation plus petites et plus détaillées, sans exiger de ressources de calcul excessives.
Plus: À propos de la sous-modélisation - Assistance utilisateur SIMULIA 2024
Maillage adaptatif
Maillage adaptatif applique un concept similaire (maillage fin dans les zones qui le nécessitent, maillage grossier ailleurs), mais il fonctionne automatiquement lors de la résolution. Grâce au maillage adaptatif, Abaqus identifie les zones où les gradients de contrainte sont élevés et affine automatiquement le maillage dans ces zones spécifiques. Cela facilite la convergence et surveille la résolution des erreurs sans avoir à analyser et mettre à jour manuellement le maillage, ni à utiliser un maillage global excessivement raffiné.
Plus: À propos d'ALE Adaptive Meshing - Assistance utilisateur SIMULIA 2024
Contrôles de maillage locaux
Au-delà de ces options, votre maillage peut être peaufiné manuellement comme et où vous le souhaitez, avec Contrôles de maillage locauxLes contrôles de maillage locaux vous permettent de saisir des tailles d'éléments spécifiques dans des zones spécifiques, selon vos besoins, tout en conservant un maillage global relativement grossier. Plutôt que de laisser Abaqus effectuer ces modifications automatiquement avec le maillage adaptatif, certains utilisateurs préfèrent le contrôle total offert par les contrôles de maillage locaux.
Plus: Affectation de contrôles de maillage - Assistance utilisateur SIMULIA 2024

Figure 15 : Corps avec maillage global grossier et contrôle de maillage local fin dans la zone d'intérêt
Abaqus offre encore plus d'options pour la sélection d'éléments et le maillage, et l'équipe GoEngineer peut vous aider à les exploiter pour créer des analyses informatives et précises. Consultez notre page « Sessions de mentorat d'application » et prendre rendez-vous avec un expert.
Conclusion
Des résultats précis de stress Abaqus sont essentiels pour des analyses techniques fiables, des améliorations de conception et la prévention des erreurs coûteuses. Les choix de maillage réfléchis minimisent les problèmes de calcul et les déformations irréalistes. Raffiner votre maillage, utiliser des formulations d'éléments appropriées et valider vos résultats par des études de sensibilité permet de vous assurer que vos études reflètent le comportement réel.
En appliquant ces meilleures pratiques, vous pouvez améliorer la fiabilité de vos modèles, ce qui vous permettra de prendre des décisions de conception plus sûres et d'améliorer la sécurité des systèmes. Une simulation bien construite ne se limite pas à générer des résultats ; elle garantit la fiabilité de ces résultats.
Formation Abaqus
Vous voulez améliorer vos compétences ? Notre catalogue de cours contient plus de 10 cours de formation Abaqus en ligne, animés par un instructeur ou à votre rythme, allant des cours d'introduction aux sujets avancés. Consultez noscatalogue de courspour plus de détails.
J'espère que ces conseils d'Abaqus Meshing pour des résultats de stress précis vous ont été utiles. EXPERIENCE d'autres trucs et astuces ci-dessous. De plus, rejoignez leCommunauté GoEngineerpour participer aux discussions, créer des messages sur le forum et répondre aux questions des autresAbaqus utilisateurs.
Articles connexes
7 conseils Abaqus/CAE pour les nouveaux utilisateurs
Solveurs Abaqus : autonomiser les ingénieurs dans tous les scénarios d'analyse par éléments finis
Comprendre Abaqus General Contact
Abaqus - Modélisation de sections transversales de poutres de forme arbitraire
Analyse de la vitesse critique et dynamique du rotor par éléments finis
À propos de Connor Bucka
Connor Bucka est un ingénieur en support technique SOLIDWORKS chez GoEngineer.
Recevez notre vaste gamme de ressources techniques directement dans votre boîte de réception.
Désabonnez-vous à tout moment.
