Réduire les exigences de calcul dans Abaqus grâce à la sous-modélisation

La taille et la complexité des conceptions de produits qui sont analysées et testées avec Abaqus – un logiciel d'analyse par éléments finis (AEF) et de simulation d'ingénierie multiphysique – continue de se développer. La sous-modélisation est une technique efficace, utilisée lorsque des résultats détaillés de simulation de produit sont requis pour une petite région localisée au sein d'un modèle plus vaste. Elle permet à l'analyste de réduire considérablement les besoins de calcul et le temps d'exécution d'une analyse.

Une analyse globale d'une structure peut d'abord servir à identifier les zones où la réponse à la charge est critique. Un sous-modèle local peut ensuite être créé pour les zones critiques, avec une représentation géométrique améliorée et/ou un maillage affiné. Ce sous-modèle local offre une précision accrue par rapport au modèle global, sans nécessiter de remaillage et de réanalyse du modèle complet. Cette approche permet de réduire les coûts d'analyse tout en conservant un niveau de détail suffisant dans les zones critiques.

Dans cet article, nous examinerons la théorie de la sous-modélisation, les deux techniques de sous-modélisation disponibles dans Abaqus et leur mise en œuvre. Nous soulignerons également les limites de la sous-modélisation dans Abaqus et l'étape importante de la vérification des résultats d'analyse.

Théorie de la sous-modélisation

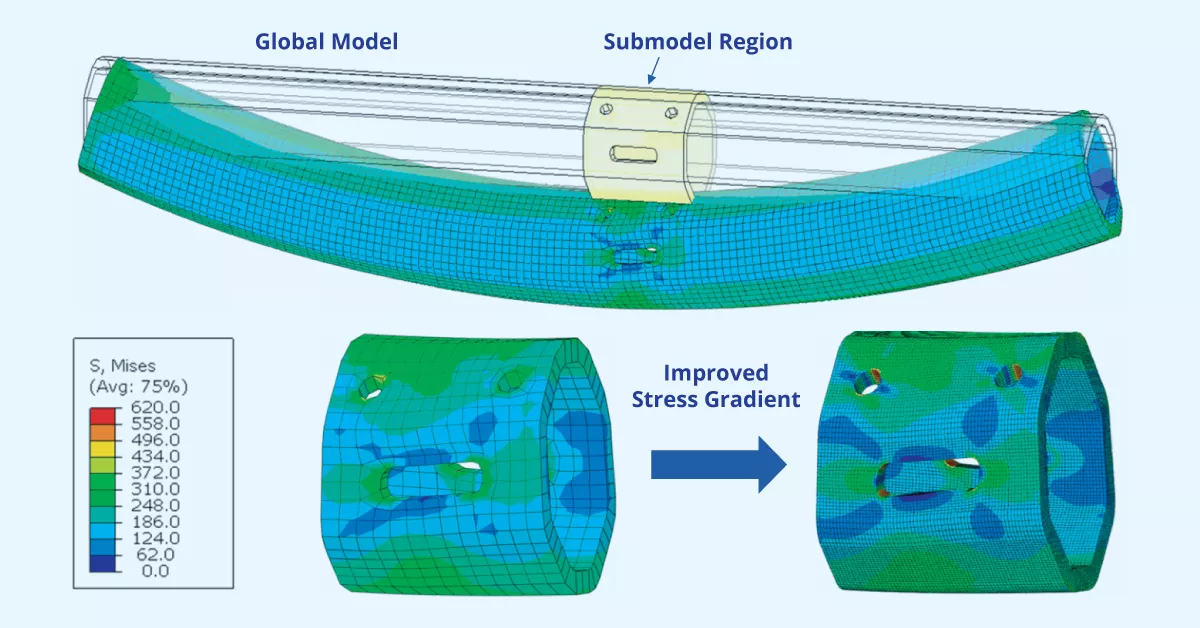
La sous-modélisation dans Abaqus utilise le principe de Saint-Venant, selon lequel la limite du sous-modèle est suffisamment éloignée de la région d'intérêt au sein du sous-modèle pour permettre le remplacement des forces appliquées par des forces locales équivalentes. La solution globale du modèle est utilisée pour définir le comportement de la limite du sous-modèle grâce au contrôle des variables pilotées qui sont représentatives des forces appliquées. La solution dans la zone d'intérêt n'est pas modifiée par les effets finaux tant que les charges finales restent statiquement équivalentes.

Français La figure 1 présente un exemple de poutre avec plusieurs ouvertures localisées. Le modèle global de la poutre complète est utilisé pour déterminer les variables pilotées en sortie aux limites communes du sous-modèle et facilite l'utilisation d'un maillage relativement grossier. Les analyses sont effectuées indépendamment sur le modèle global et le sous-modèle, les variables pilotées étant le seul lien entre les deux. Grâce à cette indépendance, il est possible de modifier les caractéristiques géométriques, les types d'éléments, les propriétés des matériaux, etc., afin d'améliorer la représentation de la région sous-modélisée. Comme pour toute technique de modélisation, il est important de valider les résultats pour s'assurer qu'ils sont physiquement significatifs. La comparaison du tracé des contours près des limites de la région sous-modélisée du modèle global et du sous-modèle peut être utilisée pour confirmer la cohérence des résultats.

Figure 1 : Modèle global et sous-modèle

Techniques de sous-modélisation dans Abaqus

Dans Abaqus, deux techniques sont disponibles pour la sous-modélisation, appelées basé sur les nœuds et basé sur la surface sous-modélisation.

Le basé sur les nœuds La technique interpole le champ de résultats nodaux du modèle global sur les nœuds du sous-modèle, c'est la technique la plus générale et la plus couramment utilisée.

Inversement, dans basé sur la surface sous-modélisation, le champ de contrainte est interpolé sur les points d'intégration de surface du sous-modèle. La sous-modélisation basée sur la surface est limitée aux applications solide-solide et à l'analyse statique ; à toutes autres fins, la sous-modélisation basée sur les nœuds doit être appliquée.

L'une ou l'autre technique ou une combinaison des deux peut être utilisée dans une analyse en fonction des attributs du modèle.

La technique basée sur la surface peut fournir des résultats de contrainte plus précis si, dans une analyse statique, il existe une différence significative dans la rigidité moyenne dans la région du sous-modèle et le modèle global est soumis à une charge contrôlée par la force. Alors que, lorsque la rigidité dans les régions est comparable, la sous-modélisation basée sur les nœuds fournira des résultats similaires à la sous-modélisation basée sur la surface avec un potentiel réduit de problèmes numériques causés par les modes de corps rigides. Des différences de rigidité peuvent survenir en raison de détails supplémentaires dans le sous-modèle tels que des ouvertures ou des congés, ou de modifications géométriques mineures qui ne justifient pas de réexécuter l'analyse globale.

Si le modèle est soumis à de grands déplacements ou rotations, la sous-modélisation basée sur les nœuds peut améliorer la précision lors de la transmission de grands déplacements et rotations au sous-modèle. Selon les résultats de sortie qui présentent le plus d'intérêt, la sous-modélisation basée sur les nœuds fournira une transmission plus précise du champ de déplacement dans le sous-modèle. Alors que la sous-modélisation basée sur la surface fournira une transmission plus précise du champ de contrainte, ce qui entraînera une détermination plus précise des forces de réaction dans le sous-modèle. Les deux techniques peuvent être incluses dans un seul modèle à différentes limites.

Mise en œuvre des sous-modèles Abaqus

Le modèle local peut être piloté à l'aide de données enregistrées dans le fichier de base de données de sortie (au format ODB ou SIM). Les sous-modèles basés sur les nœuds peuvent également être pilotés à l'aide du fichier de résultats (.fil). Seules les variables écrites dans la base de données de sortie seront utilisées dans le sous-modèle, il est donc important d'enregistrer des données de sortie adéquates à une fréquence suffisante. Ces résultats doivent être consignés dans le système de coordonnées global pour être interpolés sur le sous-modèle. Dans le cas de données nodales, les valeurs sont toujours écrites par rapport aux directions globales dans le fichier de base de données de sortie, que des transformations de coordonnées nodales soient utilisées ou non.

Toutes les variables pilotées doivent être enregistrées à une fréquence commune lors de l'analyse globale, et cette fréquence doit être suffisamment fine pour permettre une reproduction adéquate de l'historique global des variables pilotées. Si les résultats sont enregistrés à des fréquences différentes, la fréquence la plus grossière sera utilisée dans l'analyse du sous-modèle. Il est recommandé de créer un ensemble unique contenant tous les ensembles de nœuds et/ou d'éléments à partir desquels piloter le sous-modèle. Dans la figure 2, l'ensemble définissant la limite du sous-modèle est mis en évidence en rouge et étiqueté commeSous-modèle-région.

Figure 2 : Limite du sous-modèle

Tous les types de chargement prescrits et les conditions limites peuvent être appliqués au sous-modèle. Cependant, il faut prendre soin d'appliquer les charges et les conditions aux limites dans le sous-modèle d'une manière cohérente avec le modèle global afin d'éviter des résultats incorrects. Seules les variables pilotées seront interpolées et transférées au sous-modèle. Tous les champs prédéfinis doivent être fournis tels qu'ils étaient dans le modèle global.

Les conditions initiales doivent être cohérentes entre le modèle global et le sous-modèle. Pour simplifier, il peut être utile de copier le modèle global initial pour créer le sous-modèle (Figure 3), en utilisant les outils de création de coupe pour supprimer la matière en dehors des limites du sous-modèle, comme illustré dans la Figure 4. Cette approche permettra de conserver les paramètres du modèle global et de minimiser le risque d'erreurs lors de la création du sous-modèle.

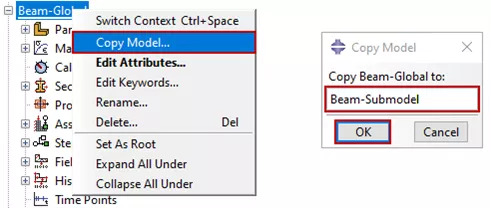
Figure 3 : Copier le modèle global pour créer un sous-modèle

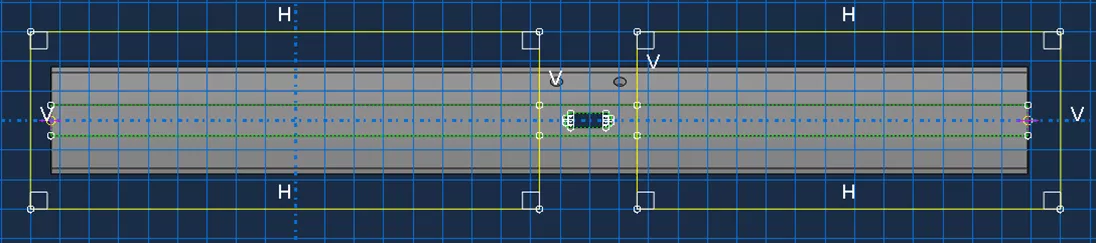
Figure 4 : Géométrie de coupe

Le temps d'étape dans l'analyse du sous-modèle doit correspondre au temps d'étape dans l'analyse globale, sinon toute interpolation par rapport au temps sera incorrecte.  En cas de divergence, la période de temps de l'étape globale peut être mise à l'échelle à celle du sous-modèle en activant l'optionÉchelle de la période de temps de l'étape globale à la période de temps de l'étape du sous-modèlelors de la mise en œuvre des conditions aux limites présentées à la figure 5.

Les nœuds pilotés sont définis via les conditions aux limites du sous-modèle. Vous pouvez spécifier les degrés de liberté à piloter à la limite du sous-modèle ; en général, tous les degrés de liberté aux nœuds pilotés sont spécifiés. Outre la mise à l'échelle de la période, Abaqus peut mettre à l'échelle la valeur des variables pilotées appliquées au sous-modèle à partir du modèle global, le cas échéant.

Dans la figure 5, une condition limite de sous-modèle est implémentée et inclut tous les degrés de liberté disponibles pour les éléments de continuum solide (1-3) sans mise à l'échelle. Notez que seules les variables de solution fondamentales peuvent être pilotées. Dans la sous-modélisation solide à solide ou coque à coque, cela inclut les déplacements, les températures, le potentiel électrique, la pression interstitielle, etc. Les vitesses ou les accélérations sur la limite du sous-modèle ne peuvent pas être pilotées. Abaqus sélectionne automatiquement les variables pilotées lorsqu'un modèle de coque global est utilisé pour piloter un modèle solide local. D'autres conditions limites de sous-modèle peuvent être créées, modifiées ou supprimées comme d'habitude.

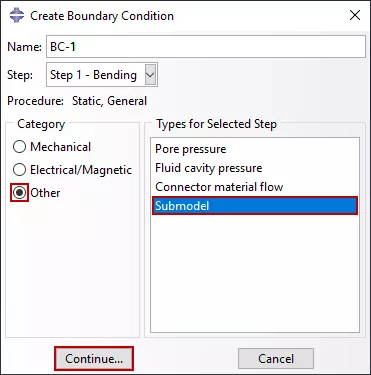
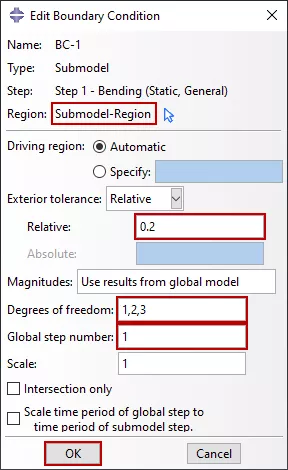
Figure 5 : Condition limite du sous-modèle

Abaqus interpole dans l'espace et dans le temps pour déterminer les valeurs des variables nodales pilotées tout au long de l'étape de l'analyse du sous-modèle. L'ordre d'interpolation spatiale des variables pilotées est dicté par l'ordre des éléments utilisés au niveau global. L'incrémentation temporelle automatique est appliquée indépendamment dans les analyses globales et de sous-modèle. L'incrémentation temporelle indépendante est supportée par l'interpolation temporelle des variables pilotées. L'interpolation temporelle linéaire est utilisée entre les valeurs lues à partir de la base de données de sortie ou du fichier de résultats.

Lorsque le modèle global subit des déplacements ou des rotations importants, l'utilisateur doit s'assurer que le sous-modèle subit également ces déplacements ou rotations. Lorsque la sous-modélisation basée sur les nœuds est utilisée, les nœuds moteurs prennent automatiquement en compte les déplacements et les rotations afin que le sous-modèle soit correctement positionné par rapport au système de coordonnées global. Inversement, pour la sous-modélisation basée sur les surfaces, l'utilisation uniquement des tractions de surface fournit au sous-modèle aucune information de déplacement.

Au lieu de cela, pour tenir compte des déplacements, le sous-modèle doit inclure : les conditions aux limites appliquées, les nœuds entraînés et le soulagement inertiel. Lorsque les deux méthodes sont utilisées, il est important de maintenir une méthode de conduite cohérente sur toute la zone sélectionnée pour éviter les surcontraintes résultant de définitions de conduite partielles ou excessives.

Lors de la configuration d'un sous-modèle, les attributs du modèle doivent être modifiés pour faire référence à la base de données de sortie ou au fichier de résultats. Les attributs du modèle illustrés à la figure 6 obligeraient Abaqus à lire leBeam-Global.odbfichier de base de données de sortie et utiliser ces résultats dans une analyse d'un sous-modèle défini dans leBeam-Submodel.inpfichier d'entrée.

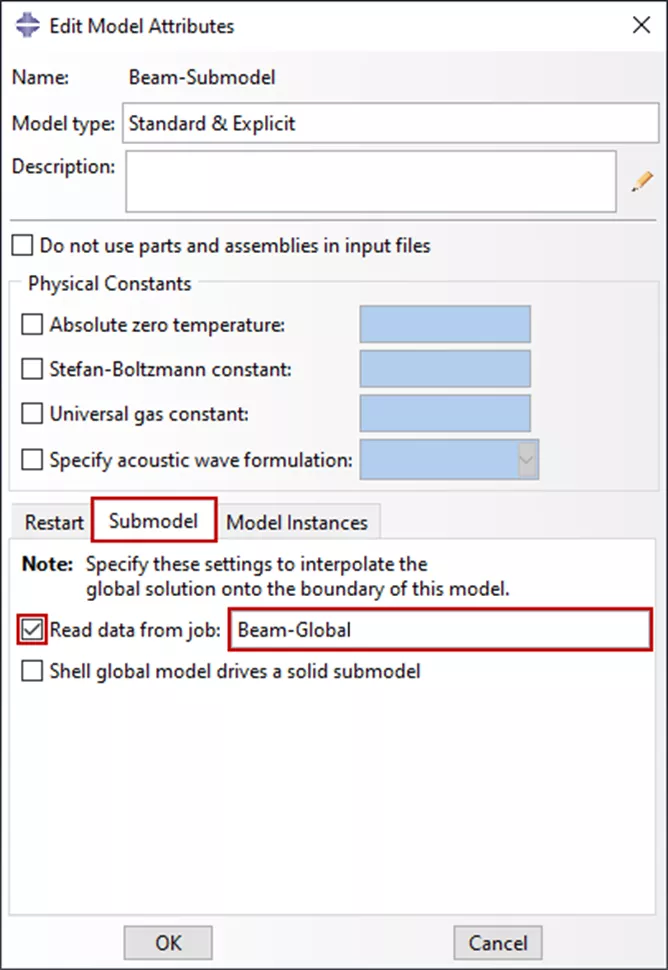
Figure 6 : Attributs du sous-modèle

Limites de la sous-modélisation

Il existe certaines limites concernant les méthodes et les types d'éléments compatibles avec l'approche de sous-modélisation. Les limitations seront brièvement décrites ici et vous trouverez plus d'informations à ce sujet dans la documentation.

Les éléments qui peuvent être utilisés aux niveaux global et sous-modèle sont limités aux éléments continus triangulaires et quadrilatéraux du premier et du second ordre, aux éléments continus de coque ou de membrane, aux éléments continus tétraédriques, en coin ou en brique du premier et du second ordre. Les modèles globaux peuvent contenir à la fois des éléments solides et des éléments de coque, à condition que tous les nœuds pilotés se trouvent dans les éléments de coque du modèle global.

Les nœuds limites du sous-modèle ne peuvent pas se trouver dans des régions du modèle global où les informations sont insuffisantes pour l'interpolation de la variable pilotée. Cela inclut les régions où il n'y a que des éléments unidimensionnels (tels que des poutres, des fermes, des liens ou des coques axisymétriques), des éléments utilisateur, des sous-structures, des ressorts, des amortisseurs, d'autres éléments spéciaux ou des éléments axisymétriques.

Lors de l'utilisation d'éléments de coque, cinq degrés de liberté par élément de coquille de nœud (S4R5, S8R5, etc.) doivent généralement être évités au niveau global car les rotations ne sont pas enregistrées. Ces éléments ne peuvent pas être utilisés dans la sous-modélisation coque-solide.

Les sous-modèles ne peuvent pas être utilisés dans les procédures couplées thermo-électriques, thermo-électrochimiques et de dynamique linéaire basée sur les modes. La sous-modélisation basée sur la surface ne peut être utilisée que dans les procédures statiques générales. La sous-modélisation coque-solide ne peut pas être utilisée avec un autre type de sous-modélisation dans le même modèle.

Vérification des résultats de l'analyse

Lors de l'utilisation de l'approche de sous-modélisation, deux ensembles de résultats d'analyse sont ensuite obtenus : le premier à partir d'un modèle global donnant une approximation du comportement, et le second à partir d'un modèle local raffiné donnant une représentation plus précise des résultats détaillés.

Une étape importante de la procédure de sous-modélisation est la vérification des résultats. La figure 7 présente les résultats d'un sous-modèle basé sur les nœuds. La cohérence des déplacements dans la région du sous-modèle est d'abord vérifiée avant de tracer le gradient de contrainte. Si des écarts majeurs sont identifiés avec les déplacements, cela affectera tous les résultats ultérieurs et le modèle devra être révisé et soumis à nouveau.

Une fois que les déplacements correspondent, d'autres sorties, comme les contraintes, peuvent être interrogées. Ici, une amélioration du gradient de contrainte est obtenue en augmentant la densité du maillage dans la région sous-modélisée. Les contraintes dans d'autres régions de la poutre peuvent être obtenues à partir du modèle global où, en l'absence d'ouvertures concentrant les contraintes, le maillage grossier est suffisant.

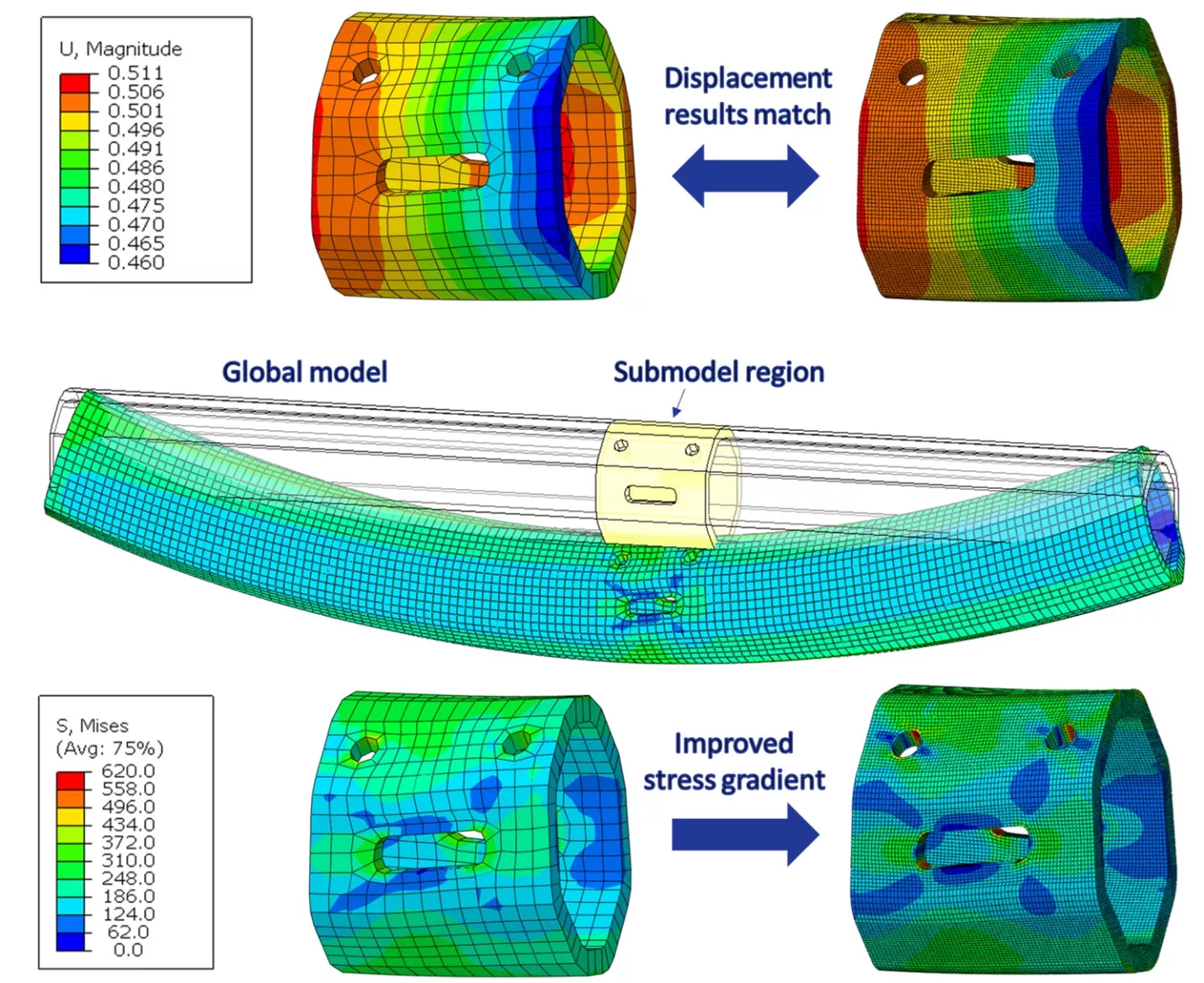
Figure 7 : Vérification des résultats

Prêt à commencer avec Abaqus ?Lisez notre guide d'achat Abaqusou Contactez-nous Pour discuter avec les experts en simulation de GoEngineer et trouver l'outil idéal, n'hésitez pas à contacter Abaqus. Si vous n'êtes pas encore prêt à utiliser Abaqus, vous pouvez néanmoins profiter pleinement de ses avantages grâce à Conseil FEA de GoEngineer.

Articles connexes

Amélioration de la conception des connecteurs pour véhicules électriques grâce à Abaqus FEA

7 conseils Abaqus/CAE pour les nouveaux utilisateurs

Les matériaux FEA sont déterminants : Aperçu de l'application d'étalonnage des matériaux 3DEXPERIENCE

Analyse structurelle par éléments finis (FEA) pour débutants : 5 étapes de la conception basée sur la simulation

Simplifier l'ingénierie : le nouveau modèle de licence unifié de SIMULIA

VOIR TOUS LES ARTICLES ABAQUS