Understanding Abaqus Material Behavior

Understanding the material behavior under different conditions is fundamental to the fields of engineering, design, and manufacturing. The sophisticated nature of material modeling in Abaqus, a leading finite element analysis software, can transform how simulation plays a role at a company. Abaqus provides the tools to model and predict a material’s response under various loading conditions, facilitating more informed decision-making processes.

In this article, we explore the various material models and see how they help in understanding the underlying mechanics. Whether you’re an experienced engineer or an aspiring analyst, join us as we delve into the fascinating world of material modeling in Abaqus, discussing everything from Elastic and Inelastic material models to more complex models such as Progressive Damage and Failure, Hydrodynamic Behavior, and Multiscale Material Modeling.

Main Material Models Used in Abaqus

Before getting into the details, it is useful to have a panoramic view of the spectrum of material models available. 

The following chart provides an overview of all the material models available in Abaqus, catering to various needs and applications. This chart should serve as a roadmap, navigating the complex terrain of material modeling in Abaqus and guiding users toward using the correct models for a specific project. 

Note: Each entry in the table is a hyperlink to its location and definition in the Abaqus documentation.

Now that we've seen the extensive range of material models available in Abaqus, let's delve a little deeper into some of the principal material models. These main models illustrate the versatility and robustness of Abaqus in handling various materials and their behaviors.

Elastic

Elastic behavior in materials refers to the ability of a material to return to its original state after being subjected to a force or stress that causes it to deform. This occurs when the applied stress does not exceed the material’s elastic limit, that is, the maximum amount of stress a material can withstand without undergoing permanent deformation.

Abaqus offers specialized material models that address unique capabilities, ranging from simple linear elastic models to more advanced ones like porous elasticity for pressure-dependent behavior, rubberlike hyperelasticity for nearly incompressible elastomers, and fabric models for the nonlinear response of woven materials.

An example of these capabilities in action can be seen in the automobile industry. The elastic models offered by Abaqus are crucial in the analysis and design of tires. By utilizing the rubberlike hyperelasticity model, manufacturers can simulate the performance of tires under various conditions, ensuring optimal grip, longevity, and fuel efficiency.

The simulation below is of a rubber bumper being compressed, comprised of a hyperelastic material model, which falls under elastic behavior.

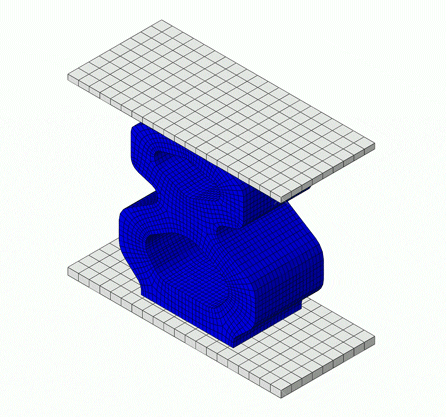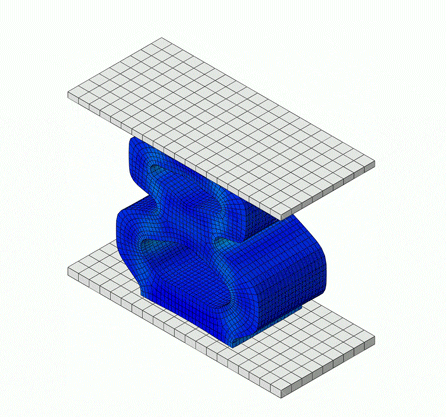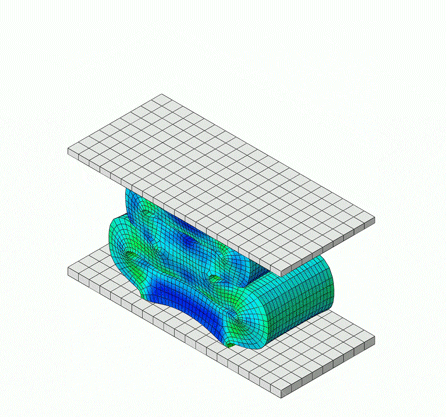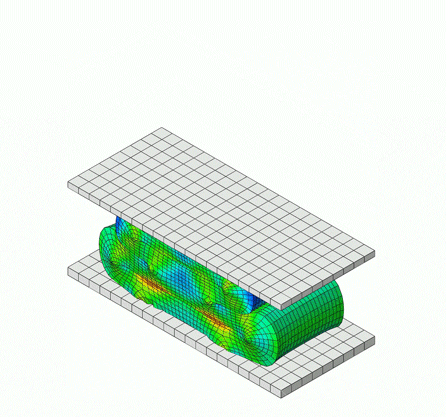
Inelastic

Inelastic behavior, also known as plastic deformation, is a property of materials that allows for permanent changes in their shape when subjected to stress. This behavior is observed in a wide range of materials, including metals, rocks, concrete, foams, and soils.

Abaqus provides an extensive library of material models to capture this complex behavior. Whether dealing with classic metal plasticity, rate-dependent yield, creep & swelling, or specialized models such as cast iron and crushable foam plasticity.

An example of these inelastic models is within the construction and infrastructure industry. For instance, understanding how materials like concrete or steel deform and yield under loads is essential for designing buildings, bridges, and tunnels.  

Below is a simulation of a twisting copper cylinder. The copper is modeled with a Johnson-Cook hardening plasticity model.

Progressive Damage and Failure

Progressive damage and failure in materials refers to the process where a material gradually loses its load-carrying capacity due to the degradation of its stiffness. This process is typically modeled using damage mechanics. 

Abaqus offers a rich set of features to predict and analyze progressive damage and failure in various types of materials. This includes a general framework for material failure modeling that allows for multiple simultaneous failure mechanisms and is designed to alleviate mesh dependency.  

An example of this is in the wind energy sector where the structural integrity of wind turbine blades, often made of composite materials, is vital. Using Abaqus' progressive damage models, manufacturers can optimize blade design, ensuring a longer lifespan and greater efficiency in harnessing renewable energy.

The simulation below is of a high-speed impact cylinder projectile and an armor plate, both of which are prone to surface erosion and damage, using the general contact algorithm in Abaqus/Explicit.

Hydrodynamic Behavior

Hydrodynamic behavior of materials refers to the response of materials to changes in pressure, volume, and temperature. This behavior is typically described using an equation of state, which is a thermodynamic equation that defines the pressure as a function of the density and the internal energy of the material.

Abaqus offers a comprehensive library of equation of state models to accurately simulate hydrodynamic behavior, including but not limited to the Mie-Gruneisen equation for high-pressure applications, the tabulated equation for sharp transitions in the pressure-density relationship, and the P-alpha for modeling the compaction of ductile porous materials.

An industry example is the evaluation of bottled packages, such as bottled water or shampoo containers. Using Abaqus' simulation capabilities, manufacturers can perform fluid-structure interaction simulations to assess how the fluid inside reacts during a drop test. This helps in understanding the integrity of the bottle, possible spillage scenarios, and the overall robustness of the packaging, ensuring that products reach consumers in optimal condition.

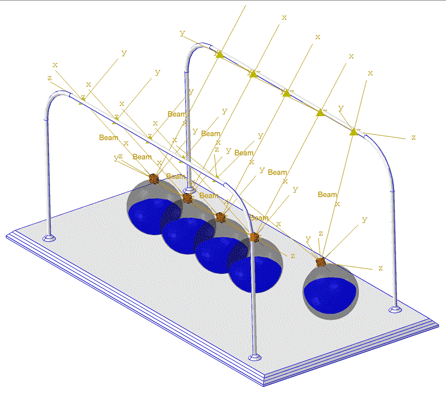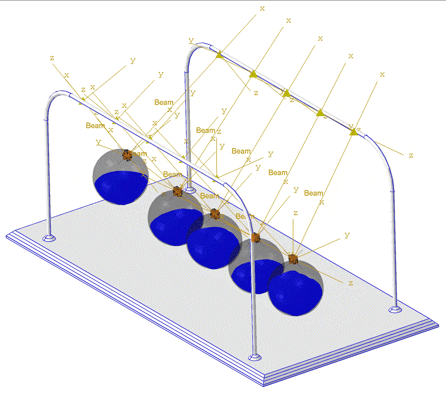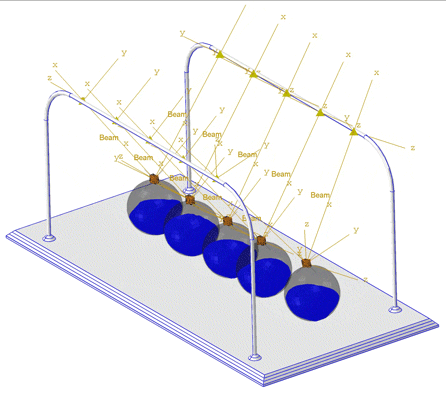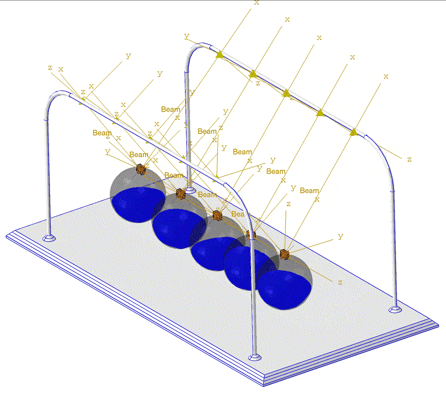
See the simulation below of a Newton cradle. The water is modeled using Eulerian elements, as a nearly incompressible fluid. The linear Us−Up Hugoniot form of the Mie-Grüneisen equation of state is used in the material model.

Multiscale Material Modeling

Multiscale modeling often involves the use of a Representative Volume Element (RVE), which is the smallest volume over which a measurement can be made that will yield a value representative of the whole material. This RVE is used to capture the microstructural heterogeneities of the material (e.g., grains, inclusions, voids, and fibers). This gives us the ability to model any arbitrarily formed composite.

Abaqus uses the mean-field homogenization approach in multiscale material modeling to efficiently predict macro-level behaviors from micro-level information. Utilizing techniques like Mori-Tanaka, it provides analytical solutions for averaged stress and strains within composites. This allows for the capture of nonlinear and history-dependent behavior, and in cases of highly nonlinear constituent materials, the software offers calibration through FE-RVE, rendering detailed microstructure representations.

 An example of this can be found in researching advanced aerospace materials. Scholars utilize Abaqus to study the microstructural variations in novel composite materials, aiming to understand their macro-level responses under stress. This deep dive into material behaviors informs the development of next-generation aircraft and spacecraft materials, promoting safety and efficiency in aviation.

The simulation below is a body-centered RVE of a composite under uniaxial tensile loading.

Example Problem

Now that we've gone through the material models, let's showcase some of Abaqus' abilities with a simple, hyperelastic model. In this simulation, we will model the rotation of one end of a bellow around a circle. The material that the below is made out of has already been characterized via four different tests: Uniaxial, Biaxial, Planar, and Volumetric. 

Depending on the type of analysis, it is not always necessary to obtain all four types of experimental test data. For instance, if you already know that your model will only be deforming in tension, then uniaxial test data will probably suffice. However, because of the type of geometry that the bellow has, it can undergo multiple forms of deformation at once. 

Model Setup

The bellow is modeled with first-order quad shell elements (S4R), where one end is fixed, while the other end is attached to a pinned center and allowed to rotate about the center. This is achieved using a beam-type connector element to maintain a constant distance. 

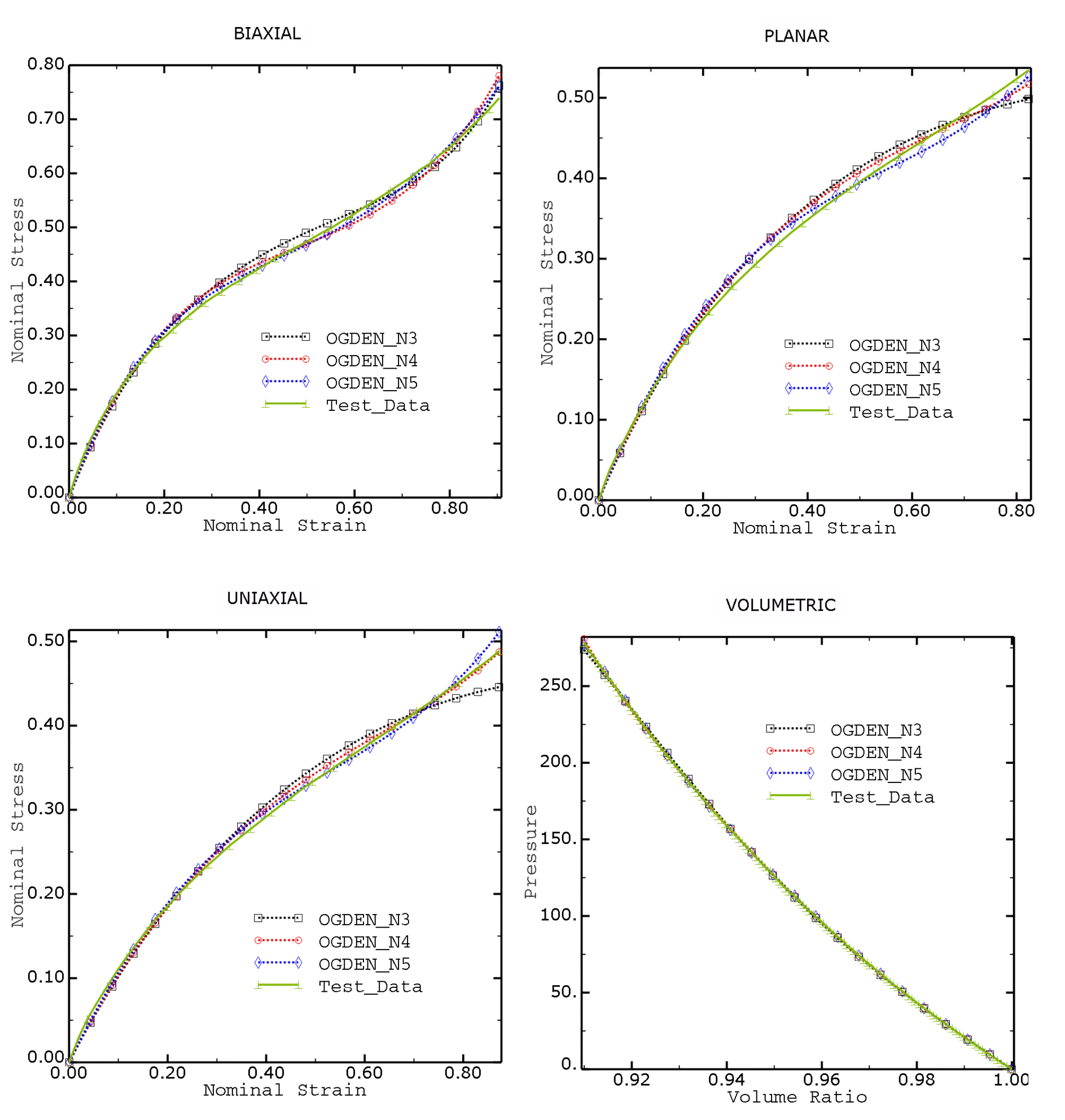
Despite having experimental material data, they still need to be calibrated to a hyperelastic model. Luckily, Abaqus comes with a calibration tool, and all the processing can be performed in the same interface, with a variety of strain energy potentials. I chose to evaluate the Ogden model of third, fourth, and fifth order, as it performs well when providing data of multiple deformation modes. 

Below are the plots that Abaqus provided after the evaluation and the coefficients for the model (not shown). The figure below also shows four subplots of Biaxial, Planar, Uniaxial, and Volumetric test data with the calibrated models. It is evident from such plots that the fourth-order Ogden model performed the best and had the closest fit to the experimental test data and, therefore, will be used. 

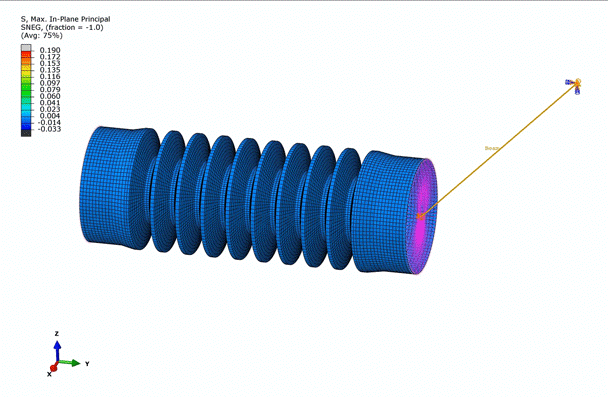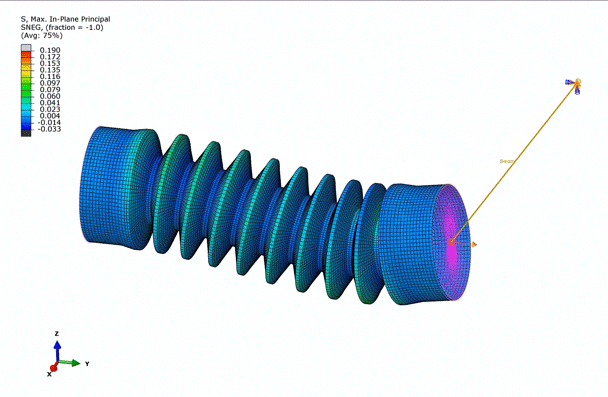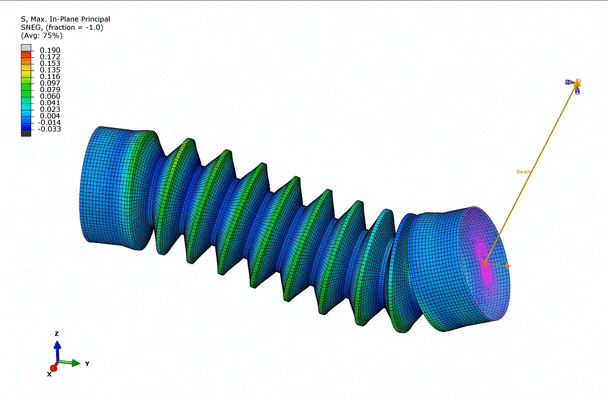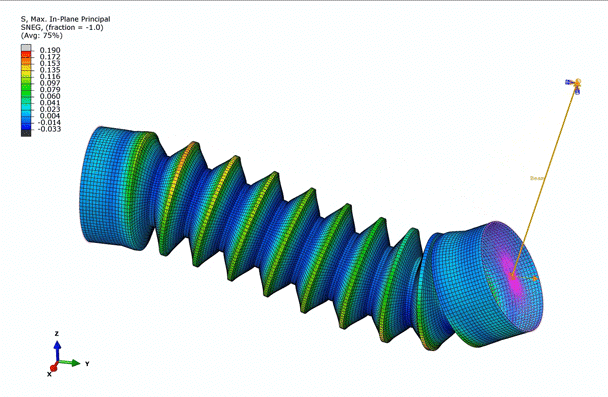
Examining the animation above, we observe that the bellow is predominantly under tension, while certain areas are in compression, dictated by the in-plane principal stresses. This observation further emphasizes the necessity to incorporate multiple deformation modes into the hyperelastic material model.

Conclusion

Abaqus offers a comprehensive suite of material models, ranging from elastic and inelastic behaviors to progressive damage and failure, hydrodynamic response, and multiscale material modeling. With its diverse capabilities, Abaqus empowers engineers and analysts to accurately simulate and predict the behavior of materials under various conditions, enabling more informed decision-making processes in engineering, design, and manufacturing projects.

Read our Abaqus buying guide or reach out to one of our GoEngineer simulation experts to find the right tool for you! If you’re not ready to use Abaqus yourself, you can still take full advantage of its benefits through FEA consulting from GoEngineer.

Related Articles

FEA Critical Speed Analysis & Rotor Dynamics

Abaqus FEA: Powerful Finite Element Modeling

Abaqus Solvers: Empowering Engineers in Every FEA Scenario

FEA and CFD Analysis Software: What to Know Before You Buy

The Ultimate Guide to Abaqus Computing

VIEW ALL ABAQUS ARTICLES